mathr / blog / #

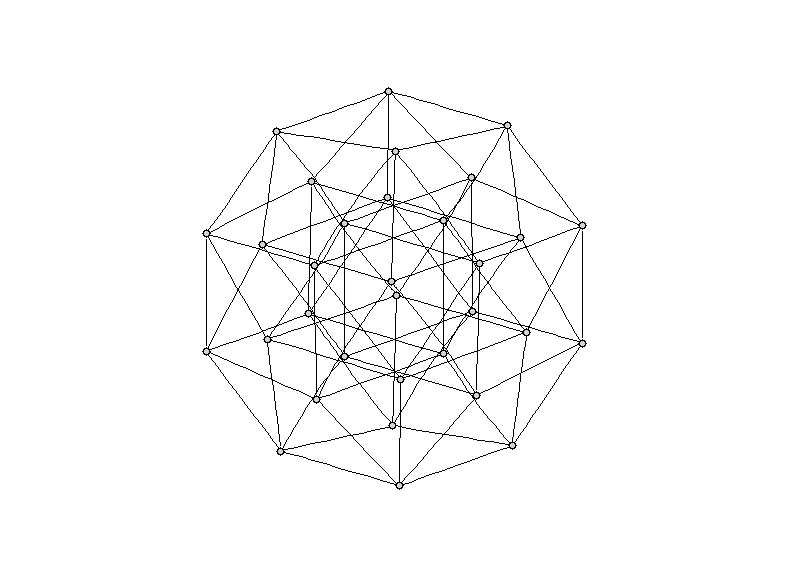
So I was toying with using Graphviz to render polytopes (higher-dimensional generalisations of polygons and polyhedra). I quickly got bored writing .dot files by hand, and switched to the Haskell programming language.

Here's some code that generates a .dot file containing the vertices and edges of a cube of arbitrary dimension:

> module Main where
> 
> import System(getArgs)
> 
> type Node = [Bool]
> 
> edges node = filter (\(u,v) -> u /= v) $ zipWith (\n b -> (n, zipWith (||) n b)) (repeat node) bits
>   where
>     bits = map bit [0..(n-1)]
>     bit b = map (== b) [0..(n-1)]
>     n = length node
>
> nodes 0 = [[]]
> nodes d = concatMap (\n -> [False:n, True:n]) ns where ns = nodes (d-1)
>
> main = do
>   args <- getArgs
>   let d = read (head args) :: Int
>       e = concatMap edges (nodes d)
>   putStrLn ("strict graph Cube" ++ (show d) ++ "D {")
>   putStrLn "  node [label=\"\",shape=\"circle\",width=0.1,height=0.1,fixedsize=true,style=\"filled\"];"
>   sequence (map printEdge e)
>   putStrLn "}"
>   where
>     printEdge (u,v) = putStrLn ("  " ++ showNode u ++ " -- " ++ showNode v ++ ";")
>     showNode n = "p" ++ map showCoord n
>     showCoord True = '1'
>     showCoord False = '0'

Above is the output for a cube of 5 dimensions, rendered with neato from Graphviz.

I also wrote code for the cross polytope (in 3 dimensions it's an octahedron):

> module Main where
> 
> import System(getArgs)
>
> type Node = Int
> 
> edges d nodes node = filter (\(u,v) -> u < v && u /= (v + d) `mod` (2 * d)) $ zip (repeat node) nodes
> 
> nodes d = [0..(2*d -1)]
> 
> main = do
>   args <- getArgs
>   let d = read (head args) :: Int
>       n = nodes d
>       e = concatMap (edges d n) n
>   putStrLn ("strict graph Cross" ++ (show d) ++ "D {")
>   putStrLn "  node [label=\"\",shape=\"circle\",width=0.1,height=0.1,fixedsize=true,style=\"filled\"];"
>   sequence (map printEdge e)
>   putStrLn "}"
>   where
>     printEdge (u,v) = putStrLn ("  " ++ showNode u ++ " -- " ++ showNode v ++ ";")
>     showNode n = "p" ++ show n

The output from neato is ugly for this structure, but with circo it looks pretty good.

The simplex is left as an exercise for the reader. These 3 (cube, cross, simplex) exist in all dimensions, when I refind my copy of Coxeter's opus I might attempt code for the others that only exist in certain dimensions.