Rolling torus
I wanted to make a smoothly looping video, which requires that the circumference of the touching circles (one on the surface of the torus, and one on the surface of the ground plane) is a rational number, ideally with small numerator and denominator. These circumferences are \(2 \pi p\) and \(2 \pi P\), so that means \(\frac{p}{P} \in \mathbb{Q}\). Call this ratio \(q\), and fix the major and minor axes of the torus \(R\) and \(r\), and its tilt angle \(\theta\). Trigonometry gives \(p = R + r \sin \theta\), which fixes \(P\).
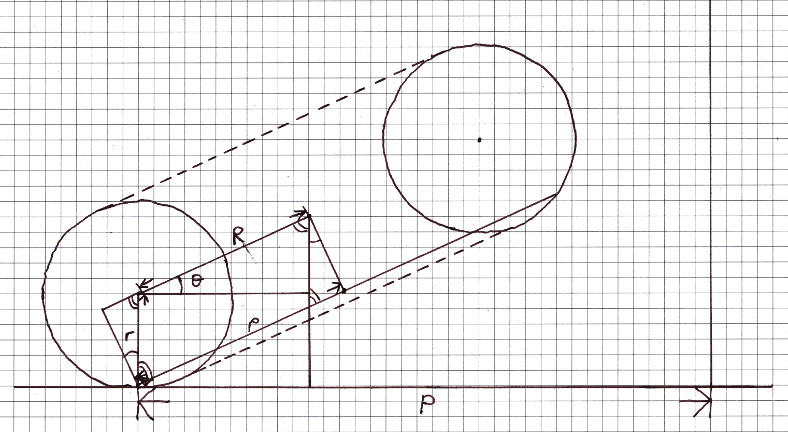
Assuming the coordinates of the centre of the circle on the ground plane are \((0,0,0)\), and fix the angular velocity \(\omega\) of the torus around that point, then the coordinates of the centre of the torus at time \(t\) are \((d \cos(\omega t), d \sin(\omega t), h)\) where \(d = P - R \cos \theta\) and \(h = r + R \sin \theta\).
The torus is in contact with the ground plane without slipping, so it must rotate about its axis when it moves. The arc length around the ground plane circle is \(P \omega t\), which must equal the arc length around the torus contact circle \(p \phi\) for some angle \(\phi\).
Solving the equations for \(\phi\) and putting these transformations together, the rolling torus is the original torus (centred on the origin) rotated \(\phi\) about the Z axis, then rotated \(\theta\) about the Y axis, then translated by \((-d,0,h)\), then finally rotated about the Z axis by \(\omega t\).
I used Fragmentarium to raytrace the video. This raytracer uses distance functions, so I needed to find the distance from the rolled torus to an arbitrary point in space - which is the same distance from the original torus to the unrolled point (just invert the chain of transformations).
The closest point on a torus to a point \(Q = (x,y,z)\) can be found by taking a vertical plane through the point and the center of the torus - reducing the problem to finding the closest point on a circle to a point. The center of that circle \(C\) is at distance \(R\) from the origin of the torus in the direction of \((x,y,0)\), and the closest point to \(Q\) on that circle is at distance \(r\) from \(C\) in the direction of \(Q - C\). The (signed) distance that gets fed to the raytracing engine is \(\left|Q - C\right| - r\).
To colour the torus, I wanted to use a conformally mapped square grid with a twist, with five hues. John M. Sullivan's paper Conformal Tiling on a Torus (Bridges 2011) gives a forward mapping from \((u,v)\) coordinates in the plane to \((x,y,z)\) coordinates in 3D space, which I needed to invert:
\[ u = \frac{s}{2 \pi} \tan^{-1}\frac{y}{x} \\ v = \frac{\mathrm{sign}(z)}{2 \pi} \cos^{-1} \frac{ z^2 \sqrt{s^2+1} \pm \sqrt{1-z^2 s^2} }{z^2+1} \]
taking the \(\pm\) to be \(+\) when \(x^2 + y^2 > R^2\), otherwise \(-\). Here \(s\) is the aspect ratio of the rectangle wrapped around the torus, which determines the lengths of its axes \(R\) and \(r\) (read the paper for the details).
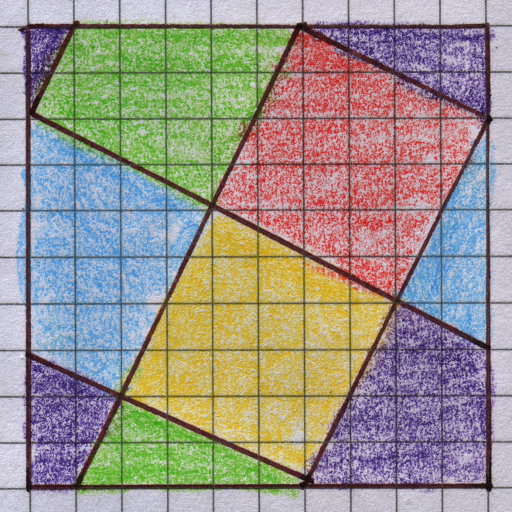
Given \((u,v)\) in a straight rectangle wrapped around the torus, the final step is to (un)twist those coordinates to the diagonal grid tiled on the rectangle, and find out which colour the pixel should be. Similar colouring is applied to the ground plane.
I had originally tried to solve the problem of the rolling torus analytically from physical principles, including energy loss through friction to allow the torus to wobble down to stillness. It was an interesting journey through inertia tensors, circular motion, angular momentum, contact friction, and so on - but rigid body dynamics are hard. I gave up on that and faked it above, but I also made a virtual physics simulation using a mesh of point masses connected with damped springs, along with some other stuff - more on that another time but there is a preview video online already.
