Implementing a 4-pole hi/lo DJ filter
In the #supercollider channel on talk.lurk.org, there was recently discussion about a "DJ filter" that transitions smoothly between low-pass and high-pass filters. This made me curious to see if I could make one. I found Miller Puckette's book section on Butterworth filters, but figure 8.18 is not quite there yet for my purposes: the normalization is off for "shelf 2" (it would be better if the Nyquist gain was 1, instead of having the DC gain as 1). The figure has 3 poles and 3 zeroes, but for simplicity of implementing with 2 cascaded biquad sections I went with a 4-pole filter design.
After fixing the order, the next variable is the center frequency \(\beta = 2 \pi f_c / SR\), which determines \(r = \tan(\beta/2)\). Using the formula from the above link gives the pole locations:
\[ \frac{(1 - r^2) \pm \mathbf{i} (2 r \sin(\alpha)) }{ 1 + r^2 + 2 r \cos(\alpha))} \]
For a 4-pole filter, \(\alpha \in \{ \frac{\pi}{8}, \frac{3 \pi}{8} \} \).
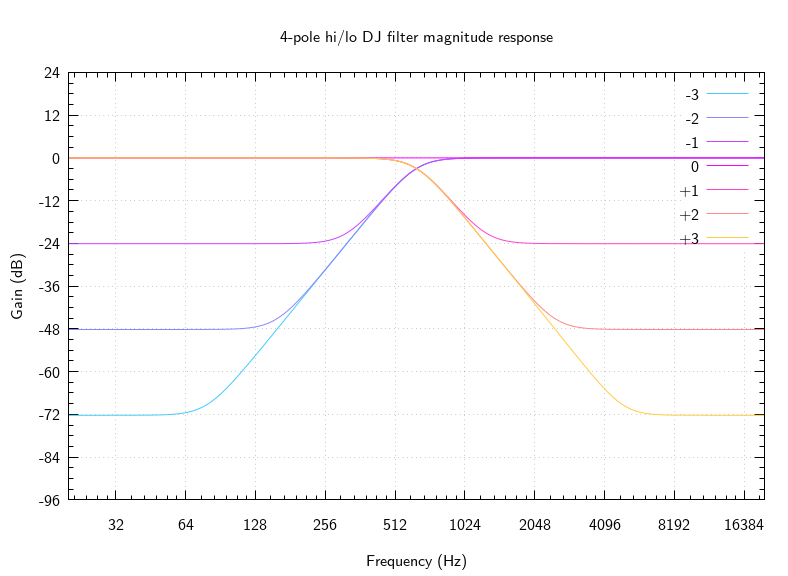
The hi/lo control \(o\) is conveniently expressed in octaves relative to the center frequency. It controls the stop band gain, which levels off after \(o\)-many octaves (so these are really shelving filters). The \(o\) control fixes the location of the zeroes of the filter, the formula is the same as above but with \(r\) modified using \(r_Z = \frac{r_P}{2^o}\).
The filter is normalized so that the pass-band gain (at DC for low-pass and Nyquist for high-pass) is unity. Then the gain in the stop band is \(-24 o\) dB, the transition slope is fixed by the order, and the center frequency gain is about \(-3\)dB when \(o\) is away from \(0\). This can be done by computing the gain of the unnormalized filter at \(\pm 1\) (sign chosen as appropriate). Computing the gain of a filter specified by poles and zeroes is simple: multiply by the distance to each zero and divide by the distance to each pole (phase response is left as an exercise).
The poles and zeroes come in conjugate pairs, which are easy to transform to biquad coefficients (see my previous post about biquad conversions). I put the gain normalization in the first biquad of the chain, not sure if this is optimal. The filters should be stable as long as the center frequency is not DC or Nyquist, as the poles are inside the unit circle. But modulating the filter may cause blowups - to be investigated.
You can browse my implementation.