# Curves

# 1 Arcs

Approximating a circular arc by a cubic Bézier curve

I needed a method that was robust in the limit of near-straight arcs as $r \to \infty$, here’s what I came up with based on fang’s answer on M.SE.

We want to approximate an arc through points $A$ and $B$ with radius $r$. If instead we have 3 points, we can use the side lengths $a, b, c$ of the triangle formed by the points to calculate $r$:

$$\begin{aligned} s &= \frac{1}{2}(a + b + c) \\ r &= \frac{a b c}{4 \sqrt{s (s - a) (s - b) (s - c)}} \end{aligned}$$

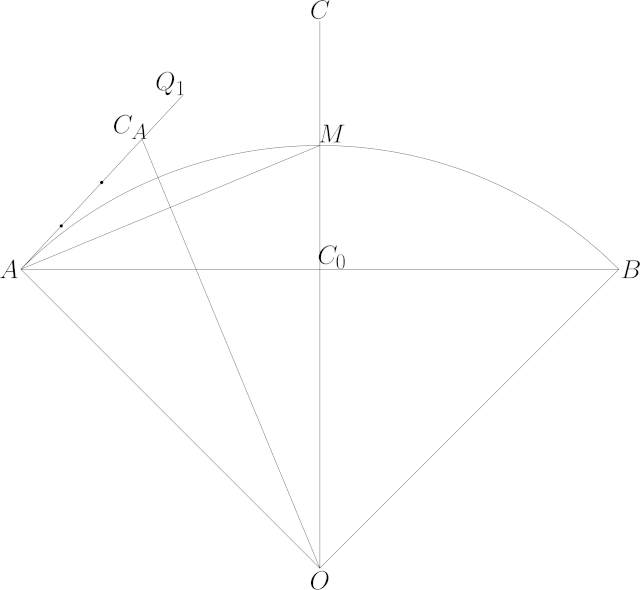
Let $C_0 = \frac{1}{2}\left(A + B\right)$ be the midpoint of $A$ and $B$. Let $C = C_0 + D$ (where $D$ is perpendicular to $AB$) be the control point of the quadratic Bézier curve through the points $A$ and $B$ with its midpoint at the midpoint of the arc, then $$|D| = 2 r \left(1 - \cos\left(\sin^{-1}\left(\frac{|A - B|}{2r}\right)\right)\right)$$ Naively computed this has catastrophic cancellation, so I used series expansion, with $x = |A - B|, y = \frac{x}{r}$: $$|D| = x y \left(\frac{1}{4} + \frac{1}{64} y^2 + \frac{1}{512} y^4 + \frac{5}{16384}y^6 + \frac{7}{131072} y^8 + O(y^{10})\right)$$ If $y$ is not small enough for the series to converge quickly enough, subdivide the original arc into smaller pieces and retry.

This quadratic Bézier is not a good approximation of a circular arc. But if we split the original arc in half (the midpoint of the arc is $C_0 + \frac{1}{2} D$), and then find the quadratic control points $C_A$ and $C_B$ for each half as above, they can be modified to give the control points $Q$ of a cubic Bézier curve for the original arc: $$\begin{aligned} Q_0 &= A \\ Q_1 &= A + \frac{4}{3}\left(C_A - A\right) \\ Q_2 &= B + \frac{4}{3}\left(C_B - B\right) \\ Q_3 &= B \\ \end{aligned}$$

A diagram may help: