# Atom Domains

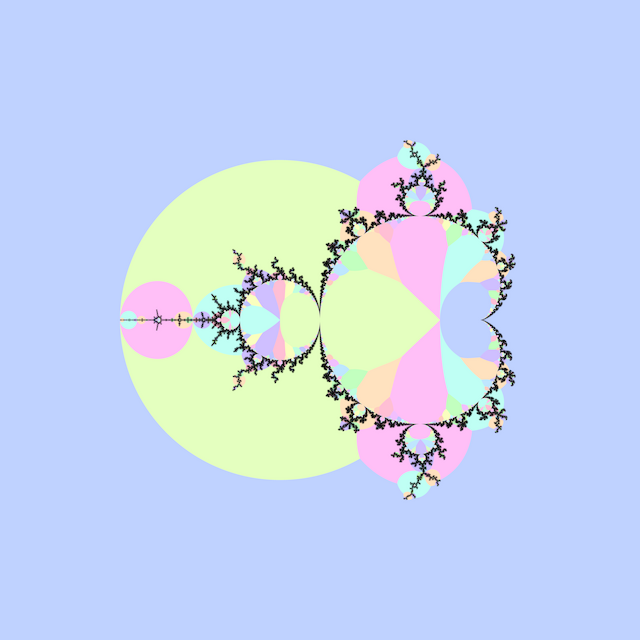
Robert P. Munafo “Atom Domain” (1996) and Heinz-Otto Peitgen and Peter H. Richter’s “The Beauty of Fractals: Images of Complex Dynamical Systems” (1986) [figure 34 on page 61] describe atom domains in the Mandelbrot set, defined as the index \(p \ge 1\) at which \(\left|z_p\right|\) is minimized during iteration of \(z_0 = 0\) and \(z_{n+1} = z_n^2 + c\). Atom domains surround hyperbolic components of the same period, and are generally much larger than the components themselves, which makes them useful for finding components.

Modified Atom Domains (2012) describes a modification of atom domains, which makes smaller domains more visible.

#include <complex.h>
#include <math.h>

int m_atom_domains(int N, double R, double _Complex c)
{
    double _Complex z = c;
    double mp = 1.0 / 0.0;
    int p = 0;
    for (int n = 1; n < N; ++n)
    {
        double zp = cabs(z);
        if (zp < mp)
        {
            mp = zp;
            p = n;
        }
        z = z * z + c;
    }
    return p;
}