# Iteration Count vs Distance Estimate
Conjectured bounds presented without proof, after some mathematical experiments in the Mandelbrot set.
# 1 Exterior
Calculate:
\[N = n + 2 - \log_2(\log(|z|^2))\]
\[d = \frac{\sqrt{|z|^2} \log(|z|^2)}{\left|\frac{dz}{dc}\right|}\]
with escape radius \(|z|^2 > 256^2\).
Plot many points in blue on a log-log scale:
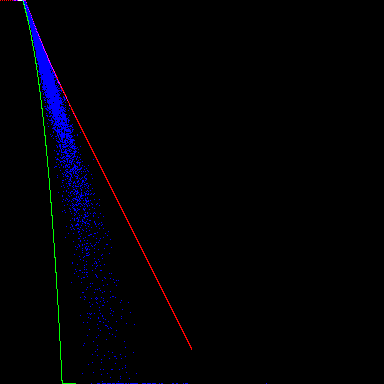
The green curve is approaching the tip of the antenna from the left, bounding like: if distance is smaller than d, iteration count must be larger than N(d). The relationship of the curve seems to be:
\[d = \frac{48}{4^N}\]
The red curve is approaching seahorse valley along an external ray, bounding like: if iteration count is larger than N, distance must be smaller than d(N). The relationship of the curve seems to be:
\[N = \frac{2.128\ldots}{\sqrt{d}}\]
Combining the bounds:
\[\frac{48}{4^N} < d < \frac{4.529\ldots}{N^2}\] \[\log_4{\frac{48}{d}} < N < \frac{2.128\ldots}{\sqrt{d}}\]
Conjecture presented without proof.
# 2 Interior
The largest component of a given period \(p = 2^k\) is probably in the period doubling cascade (iirc, need to check this…). It scales by Feigenbaum constant 4.6692… Feigenbaum constant (wikipedia). So \[ d \approx a / 4.6692\ldots^{\log_2{p}} = a / p^{2.232\ldots}\]
The smallest component of a given period \(p\) is nearest the tip of the antenna, with scaling by factor 16:
A new scaling along the spike of the Mandelbrot set, – Michael Frame, A.G. Davis Philip, and Adam Robucci, Computers & Graphics, Volume 16, Issue 2, 1992, Pages 223-234, ISSN 0097-8493, https://doi.org/10.1016/0097-8493(92)90050-6
Reprinted in
Chaos and Fractals: A Computer Graphical Journey (Chapter 40), ed. C.A. Pickover, 1998, pages 269-280, ISBN 978-0-444-50002-1 https://doi.org/10.1016/B978-044450002-1/50045-X
Child bulbs of top level cardioid scale approximately like \[\frac{1}{p^2} \sin\frac{q}{p},\] conjectured for the \(\lambda\) parameterization (which has top level discs, so no \(\sin\) factor) of \(M\) in
On the Dynamics of Iterated Maps III: The Individual Molecules of the M-Set, Self-Similiarity Properties, the Empirical \(n^2\) Rule, and the \(n^2\) Conjecture. – Benoit B. Mandelbrot, in Chaos, Fractals, and Dynamics, eds. P. Fischer and William R. Smith, 1985, ISBN 0-8247-7325-X https://archive.org/details/chaosfractalsdyn0000unse
A related conjecture is proven in
A Proof of the Mandelbrot \(n^2\) Conjecture – John Guckenheimer and Richard McGehee, Report No, 15, 1984, Institut Mittag-Leffler https://pi.math.cornell.edu/~gucken/PDF/MandelbrotN2.pdf
and the size estimate is proven in
The size of Mandelbrot bulbs – A.C. Fowler and M.J. McGuinness, Chaos, Solitons & Fractals: X, Elsevier BV, 2019, vol 3, ISSN 2590-0544 https://doi.org/10.1016/j.csfx.2019.100019
These could provide bounds on interior distance vs period. Conjecture (probably could be sharpened):
\[d < \frac{2}{p^2}\]
Bounding period the other way is not possible because \(d\) can get arbitrarily small in any component, but the size \(s\) of the smallest components (assuming they are indeed the cardioid-like one nearest -2 for each \(p\)) seems to be
\[s \approx \frac{59.2\ldots}{16^p}\]
as \(p \to \infty\), relative to the top level \(p = 1\) cardioid with \(s = 1\)..
# 3 Applications
Efficient rendering of accurate images of the Mandelbrot set with ternary colouring:
- interior
- boundary / unknown
- exterior
without wasting time iterating further if the distance is surely going to be less than a pixel.
This sort of image can provide estimates of the area of the Mandelbrot set and the box-counting dimension of its boundary.
# 4 Caveats
Don’t forget the approximate nature of distance estimates!
For bounds on square grids, you need factors of 4 in both directions, and another factor of \(\sqrt{2}\) for the diagonal vs edge of a square.
# 5 Numerical Verification
Output from a numerical search (wall-clock computation time 100mins using 16 threads on AMD 2700X CPU with 32GB RAM):
| level | total | int | bdry | ext | dim | ext00 | ext01 | ext10 | ext11 | int00 | int01 | int10 | int11 | maxn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 0 | inf | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 4 | 0 | 4 | 0 | 2.000 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 16 | 0 | 12 | 4 | 1.585 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 64 | 0 | 30 | 34 | 1.322 | 0 | 19 | 3 | 0 | 0 | 2 | 0 | 0 | 0 |
| 4 | 256 | 0 | 76 | 180 | 1.341 | 0 | 41 | 4 | 2 | 0 | 10 | 0 | 3 | 0 |
| 5 | 1024 | 28 | 204 | 792 | 1.424 | 0 | 90 | 9 | 5 | 0 | 45 | 1 | 2 | 0 |
| 6 | 4096 | 224 | 528 | 3344 | 1.372 | 0 | 232 | 25 | 16 | 0 | 127 | 1 | 7 | 0 |
| 7 | 16384 | 1144 | 1416 | 13824 | 1.423 | 0 | 585 | 70 | 73 | 0 | 310 | 4 | 14 | 0 |
| 8 | 65536 | 5246 | 3860 | 56430 | 1.447 | 0 | 1568 | 166 | 292 | 0 | 754 | 4 | 48 | 0 |
| 9 | 262144 | 22524 | 10926 | 228694 | 1.501 | 0 | 4333 | 523 | 1005 | 0 | 1722 | 13 | 124 | 0 |
| 10 | 1048576 | 93560 | 31996 | 923020 | 1.550 | 0 | 12537 | 1393 | 3600 | 0 | 4068 | 20 | 234 | 0 |
| 11 | 4194304 | 382452 | 96310 | 3715542 | 1.590 | 0 | 37071 | 3893 | 12712 | 0 | 9673 | 55 | 588 | 0 |
| 12 | 16777216 | 1549726 | 296924 | 14930566 | 1.624 | 0 | 111993 | 10828 | 44752 | 0 | 23435 | 121 | 1491 | 0 |
| 13 | 67108864 | 6246846 | 933646 | 59928372 | 1.653 | 0 | 346000 | 30231 | 157452 | 0 | 56212 | 316 | 3637 | 0 |
| 14 | 268435456 | 25101832 | 2992092 | 240341532 | 1.680 | 0 | 1083600 | 83949 | 554581 | 0 | 135398 | 753 | 9011 | 0 |
| 15 | 1073741824 | 100682952 | 9738028 | 963320844 | 1.702 | 0 | 3449490 | 234738 | 1949103 | 0 | 327014 | 1765 | 22074 | 0 |
| 16 | 4294967296 | 403399250 | 32112302 | 3859455744 | 1.721 | 0 | 11107656 | 655969 | 6860976 | 0 | 791698 | 4146 | 55611 | 0 |
| 17 | 17179869184 | 1615209248 | 107071442 | 15457588494 | 1.737 | 0 | 36149910 | 1831093 | 24174993 | 0 | 1915278 | 10132 | 143198 | 0 |
| 18 | 68719476736 | 6464740072 | 360459914 | 61894276750 | 1.751 | 0 | 118683648 | 5105618 | 85313908 | 0 | 4644022 | 24353 | 371335 | 0 |
| 19 | 274877906944 | 25868424012 | 1223643514 | 247785839418 | 1.763 | 0 | 392785193 | 14225571 | 301596356 | 0 | 11271736 | 59563 | 981405 | 4 |
- level
-
grid of 2level cells to a side
- total
-
4level
- int
-
guaranteed interior by distance estimate
- bdry
-
might contain boundary
- ext
-
guaranteed exterior by distance estimate
- dim
-
estimate of box-counting dimension of boundary
- ext00
-
counter-examples: large d, high N
- ext01, ext10, ext11
-
other cases
- int00
-
counter-examples: large d, high period
- int01, int10, int11
-
other cases
- maxn
-
potential counter-examples: high N, no d calculated as maximum iteration count was reached, no period detected
# 5.1 Potential Counter-Examples
Further analysis of the 4 unescaped potential counter-examples, with higher precision or iteration count limits, shows they are all satisfy the conjectured bound \(d < 4.5\ldots / N^2\):
precision = 100 bits
c = 3.7489700317382812500000000000000e-01 + -2.0824050903320312500000000000000e-01 i
N = 3558118.22734
d = 2.53377e-24
precision = 53 bits
c = -0.170772552490234375 + -0.827236175537109375 i
N = 2504192738.88534
d = 2.1389e-112
precision = 53 bits
c = -1.052913665771484375 + -0.252559661865234375 i
N = 6432091876.80757
d = 3.274e-121
precision = 53 bits
c = -1.072231292724609375 + -0.239337921142578125 i
N = 2155547023.15851
d = 2.0166e-276
Note: absence of known counter-examples isn’t a proof of correctness.
# 5.2 Area Estimate
The last line of the table provides an estimate for the area of the Mandelbrot set \(A_M\):
\[1.505 < A_M < 1.577\]
(Not rigorous bounds because floating point rounding isn’t taken into account, among other things.)