# Trustworthy Mandelbrot
Mathematically proven images:
white
- 100% exterior
black
- 100% interior
otherwise
- not yet determined (zone of unknown)
# 1 References
Images of Julia sets that you can trust. Luiz Henrique de Figueiredo, Diego Nehab, Jorge Stolfi, João Batista S. de Oliveira. 2013. http://webdoc.sub.gwdg.de/ebook/serien/e/IMPA_A/721.pdf
Rigorous bounds for polynomial Julia sets. Luiz Henrique de Figueiredo, Diego Nehab, Jorge Stolfi, João Batista S. de Oliveira. Journal of Computational Dynamics, 2016, 3(2): 113-137. doi: 10.3934/jcd.2016006
# 2 Algorithm
The Julia set algorithm works by interval arithmetic and cell mapping graph traversals.
The Mandelbrot set algorithm works by classifying Julia sets: if the critical point 0+0i is exterior/interior to the filled Julia set for the interval of the pixel, then the interval is exterior/interior to the Mandelbrot set.
# 2.1 Optimisations
- bit-packed quad tree saves memory (to be investigated if it saves/costs time vs byte-packed quad tree)
- storing edges as pairs of node ids in two sorted arrays (for binary search) saves memory compared to pointers and linked lists
- when constructing the graph, use one unique node for all exterior targets
- speculatively allocate a large graph and fill it in one pass, giving up on overflow, instead of calculaing size first in another pass
- uint24 for node ids in edge arrays is too slow, uint32 is less frugal space-wise but much faster
-
glibc
qsort()may allocate up to 1/4 of physical memory, which is highly undesirable when there are many threads -
naively-implemented binary most-significant-digit radix sort with uint32 keys
is very competitive time-wise with glibc
qsort() - each thread allocates all its memory up-front, and manages it internally (memory allocation/deallocation mostly follows a stack pattern, the remainder can be solved by moving the top item(s) to another stack at the other end of memory)
- store Julia sets (compressed) on OOM, to avoid having to recalculate when the concurrency is reduced and more memory is available per thread
# 3 Images












# 4 Data
# 4.1 Dump
0 / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11
This represents about 5 days of computation (wall-clock time; mostly with 16 threads active) on an AMD 2700X CPU with 32GB RAM.
# 4.2 Format
File format:
-
ASCII header contains
- magic data format identifying string
- complex interval that the image represents (currently always [-2.75,1.25]+[-2,2]i)
-
number of branch nodes in the quad tree,
from which the number of size bits for branch nodes is determined
(see
TREE_size_size_for_tree_size()intree.h, it would be better for archival if the actually used size size were stored in the file directly) - indication that binary data follows
-
header terminated by
\n\f(new line followed by form feed)
-
uncompressed bit-packed binary quad tree follows
-
sequence of 8-bit bytes, bits in little endian order in each byte
-
last byte may have unused trailing bits with arbitrary values
-
2 bits per node
- 00 red (zone of unknown)
- 01 black (100% interior)
- 10 white (100% exterior)
- 11 branch (size in units of 2 bits in even number of following bits)
-
following a branch node and its size, the 4 quadrants follow in order (bottom left, bottom right, top left, top right)
-
last two nodes of tree are unused (set to black) when the interval is symmetric about the real axis (redundancy elimination)
-
# 5 Area
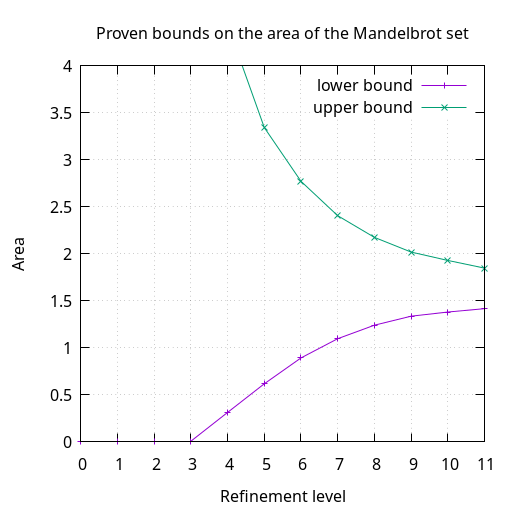
Download the data for the plot.
Level 11’s proven bounds on the area of the Mandelbrot set:
\[1.416492462158203125 \le \text{area}(\mathcal{M}) \le 1.84781646728515625\]
# 6 Source
code.mathr.co.uk/fractal-bits (subdirectory mandelbrot-trustworthy)
git clone https://code.mathr.co.uk/fractal-bits.git
cd fractal-bits/mandelbrot-trustworthy
Source code dependencies: