# mandelbrot-prelude

A Haskell library for exploring the Mandelbrot set. Works with GHC (fast) and Hugs (low resource needs). Patching some Hugs bugs is necessary for non-trivial use, see my Hugs page for details.

Still under development, no Hackage release yet.

# 1 Download

git clone https://code.mathr.co.uk/mandelbrot-graphics.git
git clone https://code.mathr.co.uk/mandelbrot-numerics.git
git clone https://code.mathr.co.uk/mandelbrot-symbolics.git
git clone https://code.mathr.co.uk/mandelbrot-text.git
git clone https://code.mathr.co.uk/mandelbrot-prelude.git

# 2 GHC

cd mandelbrot-prelude
cabal repl --ghc-options "-interactive-print pprint"

# 3 Hugs

mandelbrot-prelude/hugs.sh

# 4 API

For full list, type :browse in Hugs or GHCi.

# 4.1 Conventions

foo_ returns a list(-like) thing. foo' returns a Maybe. foo returns the value, but may call error.

Omitted contexts :: ... => can be instantiated with Double. Future work will add instances for arbitrary precision types (e.g. using the rounded package).

# 4.2 putImage

putImage renders an image of the boundary of the Mandelbrot set in black, with the background in white. The arguments are the center of the view, the vertical radius of the view, and the maximum iteration count.

> :t putImage
putImage :: Complex Double -> Double -> Int -> IO ()

> putImage (-0.75) 1.25 100
(unicode block graphics image is printed to terminal)
(it shows the whole Mandelbrot set centered in the frame)
-0.75 + 0.0 i @ 1.250e0 (100 iterations)

screenshot of whole set

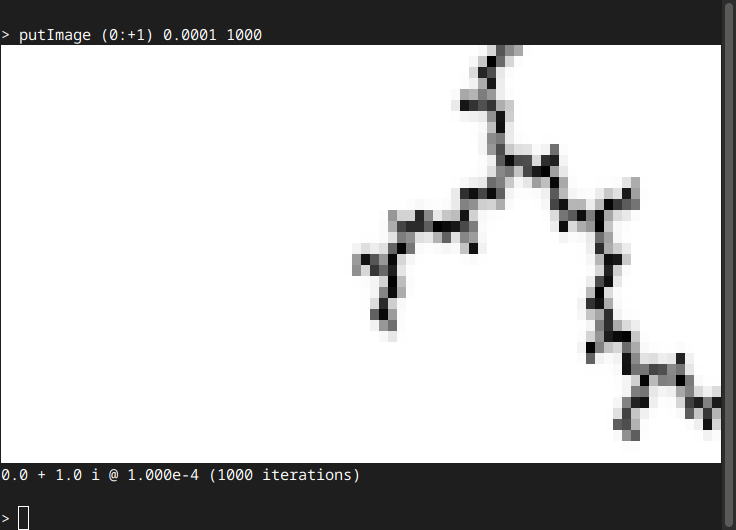
> putImage (0:+1) 0.0001 1000
(unicode block graphics image is printed to terminal)
(it shows a branching filament in the right hand half of the frame)
0.0 + 1.0 i @ 1.000e-4 (1000 iterations)

screenshot of filament near i

Video recorded using OBS of Hugs on an old Atom netbook (modern machines using GHC are significantly faster):

# 4.3 Pretty-printing

Values can be formatted to strings in Plain, HTML or LaTeX formats.

The function pprint pretty-prints in Plain format. It can be used as default print hook in GHCI.

# 4.4 Parsing

Values can be parsed from strings in Plain format using parse and parse'. To avoid the need for type annotations, many helpers are defined:

pAngledAddress :: String -> AngledAddress
pAngledAddress' :: String -> Maybe AngledAddress
pBinaryAngle :: String -> BinaryAngle
pBinaryAngle' :: String -> Maybe BinaryAngle
pBlock :: String -> Block
pBlock' :: String -> Maybe Block
pExternalAngle :: String -> ExternalAngle
pExternalAngle' :: String -> Maybe ExternalAngle
pInternalAddress :: String -> InternalAddress
pInternalAddress' :: String -> Maybe InternalAddress
pInternalAngle :: String -> InternalAngle
pInternalAngle' :: String -> Maybe InternalAngle
pKneading :: String -> Kneading
pKneading' :: String -> Maybe Kneading

# 4.5 Periods

Hyperbolic components have an associated period. Misiurewicz points have a preperiod and period. Periods and preperiods are represented with the Int type.

mandelbrot-numerics can find a period for hyperbolic component given a view:

boxPeriod :: ... => Complex r -> r -> Int
boxPeriod c r -- returns a candidate best period for a region of size r around c

There are also boxPeriod_ and boxPeriod'.

mandelbrot-symbolics has a class Period for things with (pre)periods.

class Period a where
  preperiod :: a -> Int
  period :: a -> Int
  periods :: a -> (Int,Int)
  -- specify a limit to avoid potentially long running time
  safePeriods :: Int -> a -> Maybe (Int,Int)

instance Period Periods
instance Period ExternalAngle
instance Period BinaryAngle
instance Period Kneading
instance Period InternalAddress
instance Period AngledAddress

mandelbrot-text has a newtype Periods for parsing and pretty-printing.

newtype Periods = Periods (Int, Int)

instance Period Periods
instance Eq Periods
instance Read Periods
instance Show Periods
instance Plain Periods
instance HTML Periods
instance LaTeX Periods
instance Parse Periods

# 4.6 Angles

Fractions between 0 and 1 are used to represent angles, measured in turns. Internal angles are related to the way circles are connected. External angles are related to the way the Mandelbrot set is embedded in the plane.

In mandelbrot-symbolics there is a class Q for rational numbers. The types InternalAngle and ExternalAngle are instances of it. However mandelbrot-numerics requires the standard Haskell Prelude.Rational. You can convert between them using fromQ and toQ.

# 4.7 Parents and children

Found in mandelbrot-numerics, operations on adjacent circles and cardioids:

data Child r = Child Int (Complex r) -- period and center

Find child at internal angle t from parent with period p and center c:

child :: ... => Int -> Complex r -> Rational -> Child r
child p c t

Find a chain of descendants:

children :: ... => Int -> Complex r -> [Rational] -> [Child r]

The operation can work in reverse to find a chain of parents to the nearest cardioid:

data Parent r
  = NoParent (Complex r) -- cusp
  | Parent (Complex r) Rational Int (Complex r) -- bondpoint angle period nucleus

parent :: ... => Int -> Complex r -> Parent r
parents :: ... => Int -> Complex r -> [Parent r]

Examples:

> mapM_ print $ children 1 0 [1 % 2, 2 % 3, 3 % 4]
Child 2 ((-1.0) :+ 0.0)
Child 6 ((-1.13800066665096) :+ (-0.240332401262098))
Child 24 ((-1.11384727389476) :+ (-0.253483319236841))

> mapM_ print $ parents 24 ((-1.11384727389476) :+ (-0.253483319236841))
Parent ((-1.11523274434712) :+ (-0.252762839726454)) (3 % 4) 6 ((-1.13800066665096) :+ (-0.240332401262098))
Parent ((-1.125) :+ (-0.21650635094611)) (2 % 3) 2 ((-1.0) :+ 0.0)
Parent ((-0.75) :+ 1.22464679914735e-16) (1 % 2) 1 (0.0 :+ 0.0)
NoParent (0.25 :+ 0.0)

# 4.8 Angled internal addresses

Angled internal addresses identify hyperbolic components via chain of wakes. They consist of a list of periods (strictly increasing) separated by internal angles. Not all angled internal addresses are realizable in the Mandelbrot set.

As the Plain format for AngledAddress is awkward, there is ConciseAddress:

newtype ConciseAddress = ConciseAddress AngledAddress
unConciseAddress :: ConciseAddress -> AngledAddress
pConciseAddress :: String -> ConciseAddress
pConciseAddress' :: String -> Maybe ConciseAddress
pAddress :: String -> AngledAddress
pAddress' :: String -> Maybe AngledAddress

The format can omit many angles that are 1/2, and omits periods resulting from multiplying by a denominator.

Example:

> pprint $ pAddress "1 2 3 1/3 1/2 10"
1_1/2->2_1/2->3_1/3->9_1/2->10

Angled internal addresses can be converted to and from external angles:

> pprint . addressAngles . pAddress $ "1 2 3 1/3 1/2 10"
(147/341,454/1023)

> pprint . angledAddress $ 147%341
1_1/2->2_1/2->3_1/3->9_1/2->10

There are ' versions too that return Maybe.

A final list of angles can be split from an address; it’s more efficient to trace external rays to a cardioid, then find child circles, instead of trying to trace external rays to a circle directly:

splitAddress :: AngledAddress -> (AngledAddress,[InternalAngle])
joinAddress :: AngledAddress -> [InternalAngle] -> AngledAddress

# 4.9 Tracing external rays

The ExternalAngle type is rational, while the BinaryAngle type is binary. Convert between them with binary and rational. Convert between pairs of them with binary2 and rational2.

External angles parameterize external rays, which can be traced from a large radius in towards the Mandelbrot set.

Example:

> mapM_ print . Prelude.take 32 . exRayIn 4 $ 4 % 15
(-6850.37736870893) :+ 65176.9869348552
(-2728.76499994794) :+ 25962.4647194314
(-541.063590680585) :+ 5147.8761946454
(-138.782724720925) :+ 1320.42942294493
(-44.2016895430127) :+ 420.550983804623
(-17.3889414599879) :+ 160.686005466489
(-8.02059022579482) :+ 71.5501804463158
(-4.30913074098224) :+ 36.2346340462539
(-2.65013204939833) :+ 20.4450457240978
(-1.82816775622328) :+ 12.6314128320829
(-1.38470278904755) :+ 8.42044008568637
(-1.12625861951356) :+ 5.98178473080862
(-0.964603724826411) :+ 4.48116235377119
(-0.856231753402985) :+ 3.50928708770253
(-0.778415830964795) :+ 2.85229235706047
(-0.71865723088116) :+ 2.39207139296338
(-0.669882666942511) :+ 2.06017448966566
(-0.628008155192409) :+ 1.81515633774386
(-0.590669186732474) :+ 1.63091221534286
(-0.556508906230607) :+ 1.49037348604655
(-0.524768699196137) :+ 1.38199595148228
(-0.495036538047215) :+ 1.29772369994397
(-0.467087475030156) :+ 1.23178289574069
(-0.440795709626534) :+ 1.17994312560235
(-0.41608633484741) :+ 1.13905153972917
(-0.392914387154241) :+ 1.10672250334482
(-0.371254651889233) :+ 1.08112142550428
(-0.351089275547205) :+ 1.0608145242068
(-0.332395858352319) :+ 1.04466649002643
(-0.315136877495458) :+ 1.03177540855617
(-0.299255931398186) :+ 1.02143127779518
(-0.284678961596266) :+ 1.01308705860628

The first parameter is the sharpness: how many steps to take within each dwell band.

The “end” of the ray can be used as an initial guess for Newton’s method in the nucleus or misiurewicz functions. Usually going twice the total of the preperiod and period, multiplied by the sharpness, steps is enough: but this is not proven to be safe always.

Example:

> nucleus 4 . (!! (4 * 2 * 4)) . exRayIn 4 $ 4 % 15
(-0.156520166833755) :+ 1.03224710892283

> misiurewicz 3 1 . (!! (4 * 2 * 4)) . exRayIn 4 $ 1 % 4
(-0.228155493653962) :+ 1.11514250803994

Note: the preperiod 3 of the Misiurewicz point is one more than the preperiod 2 of the angle 1 % 4:

> periods (1 % 4 :: ExternalAngle)
(2,1)

# 4.10 Enumerating components

The easiest way to enumerate components of period p is via external angles. Try all numerators with denominator 2^p - 1. Ensure the period of the angle is p. Two rays land on each component’s root, so to avoid listing each component twice, convert to angled internal address, convert back to a pair of external angles, and check our angle is the lower angle. Then trace the external ray and find the nucleus. Given the period and nucleus, the size can be calculated. Finally render the locations.

Example: save as p5.hs, run with mandelbrot-prelude/hugs.sh p5.hs:

import Mandelbrot.Prelude

main = sequence_
  [ putImage c r 1000 >>
    pprint a >>
    pprint (binary lo) >>
    pprint (binary hi) >>
    putStrLn ""
  | let p = 5
  , let d = 2^p - 1
  , n <- [ 1 .. d - 1 ]
  , let t = n % d :: ExternalAngle
  , period t == p
  , let a = angledAddress t
  , let (lo, hi) = addressAngles a
  , t == lo
  , let sharpness = 8
  , let e = exRayIn sharpness (fromQ t) !! (2 * sharpness * p)
  , let c = nucleus p e
  , let r = 2 * magnitude (size p c)
  ]