# Wedged

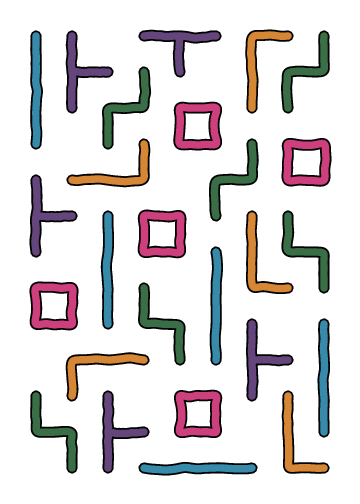
Wedged

Copyleft: This is a free work, you can copy, distribute, and modify it under the terms of the Free Art License.

The concept for Wedged is “playing Tetris optimally badly”. Badly in that no row is complete, and optimally in that each row has at most one empty cell, and the rectangle is filled. The implementation is in Haskell, now compatible with both GHC and Hugs. The program takes a few minutes to run, generating a couple of hundred images totalling a few 10s of MB. The arrangement of pieces is the same on each run, but the uneven wobbly hand-drawn appearance is randomized and different each time.

The full source code is several hundred lines long, all in one file, with few comments or documentation. The architectural overview is this: Starting from an empty rectangle, block off one cell in each row, subject to the constraint that blocked cells in nearby rows shouldn’t be too close to each other, and the blocked cells should be roughly evenly distributed between columns. Some of these blockings might be duplicates (taking into account mirroring and rotation), so pick only one from each equivalence class.

Starting from the top left empty cell in each of these boards, fill it with pieces that fit. Fitting means that the piece is entirely within the board, not overlapping any blocked cells or other pieces. There are some additional constraints to improve aesthetic appearance and reduce the amount of output images: there should not be too many pieces of the same colour in the board, all adjacent pieces should be a different colour, and no piece should be able to slide into the space left when blocked cells are removed (this applies only to the long thin blue pieces, the other pieces can’t move due to the earlier constraint on nearby blocked cells). The implementation uses MonadPlus [] for tree search with pruning, giving a list of possible fillings.

The filling process has some other aesthetic constraints: the board must be diverse (there must be a wide range of distinct colours in each row and column), the complete board must have a roughly even number of pieces of each colour, and there shouldn’t be any long straight line boundaries between multiple pieces. The complete boards might have duplicates under symmetries (in the case that the original blocking arrangement was symmetrical), so pick only one from each equivalence class.

Finally each board is visualized. The pieces are extracted from the board using a horrific function 75 lines long, which performs brute force case analysis to determine the orientation of each piece and how to draw it (whether a sequence of lines for most pieces, or a closed loop for the red squares). The actual drawing uses recursive randomized midpoint perturbation to make each stroke wobbly, then uses the painter’s algorithm to outline it: first a thick black stroke is drawn, followed by a narrower coloured stroke. The coloured pieces are drawn on a white background rectangle, with some margin space, and the result is saved to a numbered output file.

You can install Wedged from Hackage, or browse code.mathr.co.uk/wedged.

git clone https://code.mathr.co.uk/wedged.git