mathr / blog / #

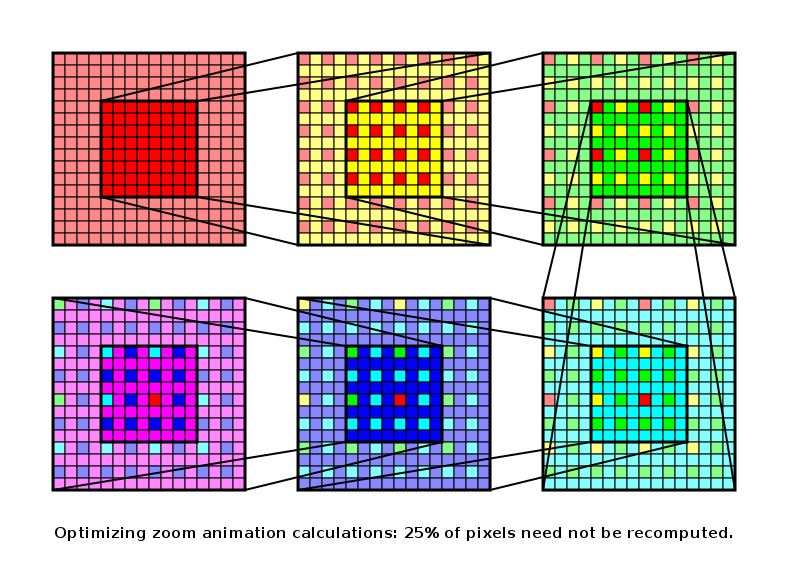
Suppose one has a generative image, as a function from position to colour. Some such images are interesting enough to want to be able to generate animations zooming in to a particular point. For example, the Mandelbrot Set is one such interesting generative image. Suppose you zoom in by a factor of two: it turns out that you can re-use pixels computed at the previous zoom level, which means you don't have to recompute 25% of the new image.

Furthermore, to generate smoother appearance for images with lots of fine details, one generally wants to oversample to reduce aliasing artifacts: that is, one computes more than one point per pixel. Now supposing you have sufficiently oversampled your images, and generated a zoom image sequence with a twofold zoom between each consecutive pair of images, you can interpolate between scaled versions of these oversampled images, so as to maintain a constant points-per-pixel density: this should in theory generate a smooth zoom animation, with much less computation than calculating each pixel of each frame.

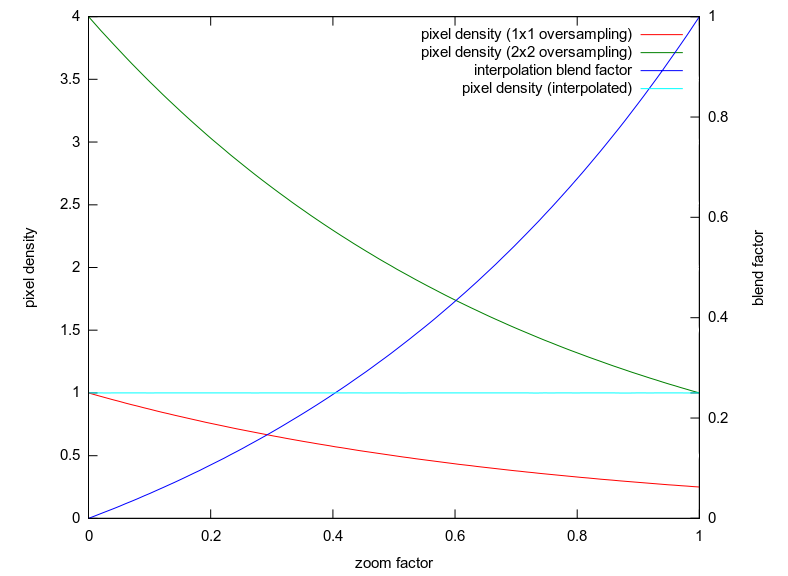
The optimal (in terms of maintaining constant points per pixel) blend factor for t in [0..1] with zoom 2^t turns out to be:

b(t) = (1 - 4^(-t)) / (4^(1-t) - 4^(-t))

Suppose one wants 4x4 oversampling at a frame size of 788x576, to generate a zoom animation lasting 5mins at 25fps with a final zoom factor of 2^64 compared to the first frame. The standard method would compute:

5 * 60 * 25 * 4 * 4 * 788 * 576 = 54,466,560,000 points

5 * 60 * 25 = 7,500 image downscales

0 image blends

The optimizations described above would compute:

64 * 2 * 2 * 4 * 4 * 788 * 576 * 3 / 4 + 1 * 2 * 2 * 4 * 4 * 788 * 576 * 4 / 4 = 1,423,392,768 points

5 * 60 * 25 * 2 = 15,000 image downscales

5 * 60 * 25 = 7,500 image blends

The 97% reduction in the number of points that need to be calculated should hopefully outweigh the additional costs of downscaling and blending.