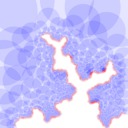
Circular wavefronts
I implemented yet another method to visualize the Mandelbrot Set in Haskell, using circles around points with radius their distance estimate divided by 4 (ensuring no points of the Mandelbrot Set are inside that circle), starting new circles where they intersect.
The algorithm in Haskell:
algorithm :: Integer -> Rectangle -> Set Circle -> Set Circle -> IO ()
algorithm count bounds active inactive = do
when (((2 ^) . round . logBase 2 . fromIntegral $ count) == count) $ do
writeFile (show count ++ ".svg") (toSVG bounds active inactive)
case S.maxView active of -- Ord Circle is by radius and then (arbitrarily) center
Nothing -> do
c <- randomBorderPoint bounds
case distance . refine . vertex $ c of
Nothing -> algorithm (count + 1) bounds active inactive
Just d -> algorithm (count + 1) bounds (S.singleton (Circle c (d/4))) inactive
Just (me, rest) -> do
let them = S.toList $ rest `S.union` inactive
new = S.fromList
[ Circle q (d/4)
| q <- concatMap (intersect me) them
, q `inside` bounds
, all (q `outside`) (map shrinkSlightly them)
, let md = distance . (!!(2^(4::Int))) . iterate refine . vertex $ q
, isJust md -- very highly likely, but better safe...
, let Just d = md
]
algorithm (count + 1) bounds (new `S.union` rest) (me `S.insert` inactive)It's not the fastest algorithm in the world...