mathr / blog / #

A short fractal video loop rendered with continuous escape time for an iterated function system.

The Generator for this iterated function system is three lines in a zigzag:

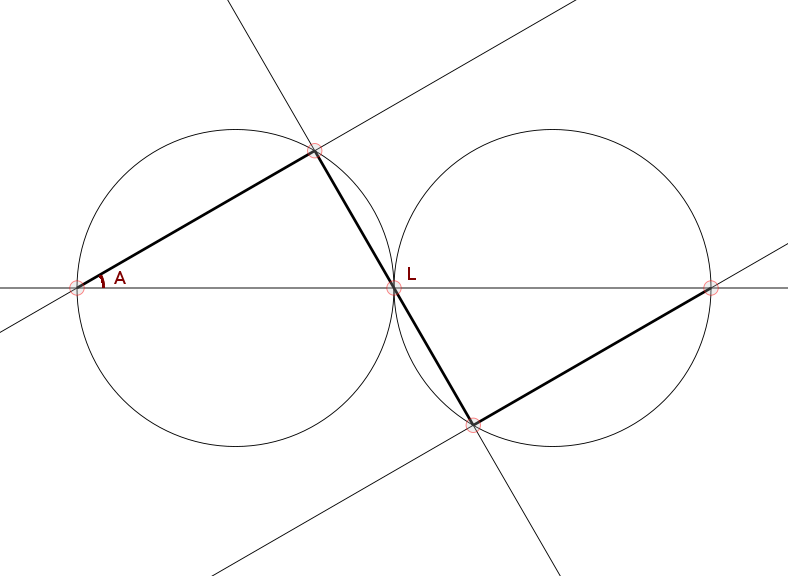
Given the fractal dimension D (between 1 and 2), the length L (between 0 and 1) of the middle line segment can be calculated by finding a root (either by standard numerical methods, or by binary search as the function is strictly monotonic) of:

2 * (sqrt ((1 - L^2) / 4))^D + L^D - 1 = 0

The Affine Transformations (each T_i expressed as a 3x3 matrix using homogeneous coordinates) that take the whole to the parts are calculated by:

T_i = post * M(a_i, l_i, v_i) * pre

a₁ = pi/2 - acos L

a₂ = - acos L

a₃ = a₁

l₁ = sin (acos L) / 2

l₂ = L

l₃ = l₁

v₁ = (0, 0)

v₂ = (l₁ * cos a₁, l₁ * sin a₁)

v₃ = (1, 0) - v₂

M(a, l, (x, y)) = (c, s, x; -s, c, y; 0, 0, 1) where c = l * cos a, s = l * sin a

post = M(0, 1, (-0.5, 0))

pre = M(0, 1, (0.5, 0))

Continuous Escape Time for an iterated function system is defined (for points not in its attractor) by:

E(x)

= 0, ||x|| >= R;

= max_i{ (log R - log ||x||) / (log ||F_i^-1(x)|| - log ||x||) }, ||x|| < R, ||F_i^-1(x)|| >= R for all i

= 1 + max_i{ E(F_i^-1(x)) }, otherwise

which can be described as the length of the longest path that escapes beyond a circle of radius R. Computing this on a per-pixel basis by exhaustive search through all paths takes O(m^n) time, where m is the number of functions in the system and n is the eventual escape count.

A Faster Method Of Computation taking O(m*n) time, can be achieved by rasterizing a square big enough to contain a circle of radius R centered on the origin, initially filled with the first two cases of the escape time equation E(x), and incrementally refining it by accumulating the effects of each transformation in parallel. This approach lends itself well to GPU-based computation, though the images are less accurate (noticeably blurrier) than per-pixel recursion.

To determine the number of incremental refinement passes to perform, an estimate can be derived from the largest contraction factor and a desired accuracy (eps = 0.001 for example):

l_max = max_i{ l_i }

passes = ceiling (log_lmax eps)

The Initialisation Pass fills a raster, where er = R and rho = l_max, using -1 as a sentinel for unknown values:

uniform float er;
uniform float rho;

void main() {
  vec2 p = er * (gl_TexCoord[0].xy * 2.0 - vec2(1.0));
  float l = length(p);
  float n;
  if (l >= er) {
    n = 0.0;
  } else if (er > l && l >= rho * er) {
    n = (log(er) - log(l)) / -log(rho);
  } else {
    n = -1.0;
  }
  gl_FragData[0] = vec4(n);
}

The Refinement Passes accumulate transformations (each ts[i] is the matrix inverse of T_i):

uniform sampler2D src;
uniform float er;
uniform mat3 ts[3];

void main() {
  vec2 p0 = er * (gl_TexCoord[0].xy * 2.0 - vec2(1.0));
  float m = -1.0;
  for (int i = 0; i < 3; ++i) {
    vec3 p = ts[i] * vec3(p0, 1.0);
    vec2 q = p.xy / p.z;
    float l = length(q);
    if (l < er) {
      m = max(m, texture2D(src, (q / er + vec2(1.0)) / 2.0).x);
    }
  }
  if (m >= 0.0) {
    m += 1.0;
  }
  m = max(m, texture2D(src, (p0 / er + vec2(1.0)) / 2.0).x);
  gl_FragData[0] = vec4(m);
}

The usual GPGPU-style ping-pong technique between textures bound to frame buffer objects is used here.

The Colouring Pass assigns colours to the escape times, where speed = 2 pi / passes:

uniform sampler2D src;
uniform float speed;

void main() {
  vec2 p = gl_TexCoord[0].xy;
  float n = texture2D(src, p).x * speed;
  vec3 yuv;
  if (n < 0.0) {
    yuv = vec3(0.0);
  } else {
    yuv = vec3(clamp(log(1.0 + n / 4.0), 0.0, 1.0), 0.125 * sin(n), -0.125 * cos(n));
  }
  vec3 rgb = yuv * mat3(1.0, 0.0, 1.4, 1.0, -0.395, -0.581, 1.0, 2.03, 0.0);
  gl_FragData[0] = vec4(rgb, 1.0);
}

Cropping to the interesting region can be performed by manipulating texture coordinates in the colouring pass:

drawCropped er = renderPrimitive Quads $ do
    t (0.5-tx) (0.5+ty) >> v 0 1
    t (0.5-tx) (0.5-ty) >> v 0 0
    t (0.5+tx) (0.5-ty) >> v 1 0
    t (0.5+tx) (0.5+ty) >> v 1 1
  where
    aspect = 16/9  -- window aspect ratio
    tx = 1 / (2 * er)
    ty = 1 / (2 * er) / aspect
    t, v :: GLdouble -> GLdouble -> IO ()
    t x y = texCoord (TexCoord2 x y)
    v x y = vertex (Vertex2 x y)

Benchmarks: it took around 12 minutes to render 375 frames of 1280x720 video with D varying from 1 to 1.75 and R = 8 with 8192px square 1-channel float textures on an NVIDIA GTX 550Ti.

References:

continuous escape time

"Rendering Methods for Iterated Function Systems" D Hepting, P Prusinkiewicz