Escher's Butterflies

I stumbled across M C Escher's "Circle Limit With Butterflies" on wikipaintings.org and thought it was awesome, related to some conformal pictures I'd made recently (more on that another time...). Its construction intrigued me, so I unwrapped from a circle to a flat strip:

First I noticed it was a simple hexagon/square/triangle tiling, albeit with curved edges from interlocking rings - but then it struck me that the colouring wasn't as symmetrical as it could have been. The rings of the same colour are situated in rectangles when they could have been in triangles, so I scribbled some diagrams on paper to work out the geometric transformations and their accompanying colour permutations. I then implemented it in 300-odd lines of Haskell and GLSL using OpenGL, and post-processed the images in GIMP to make them look nicer:


So, how does it work? Each butterfly is in a trapezoid tile, with rotational symmetries around three points on its boundary - six-fold at the top left corner, three-fold at the bottom right corner, and two-fold at the top above the bottom right corner:
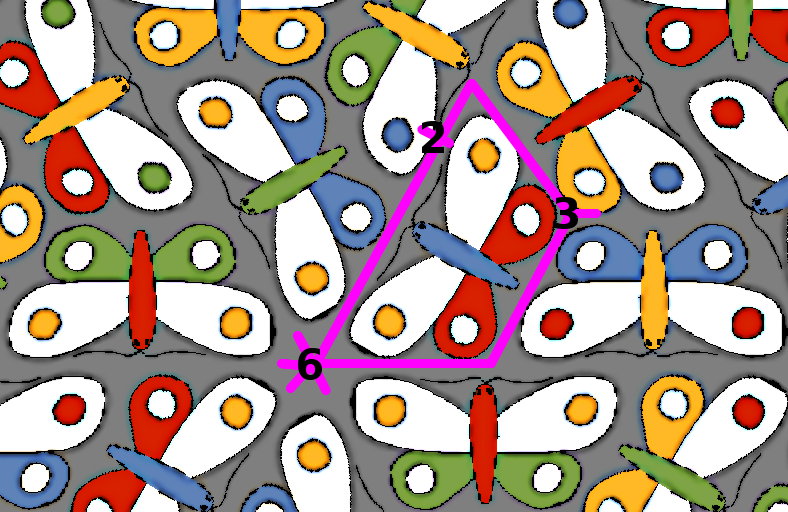
Each of these clockwise rotations has a corresponding colour permutation:
6 : (body, spots, wings, unused) → (wings, spots, unused, body)
3 : (body, spots, wings, unused) → (wings, body, spots, unused)
2 : (body, spots, wings, unused) → (spots, body, unused, wings)
So when finding the transitive closure of the transformations to fill (the visible part of) the plane with butterflies starting from a seed butterfly, carry along the current colour permutation too.
The end result for each butterfly is a 3x3 geometric transformation matrix (using 2D homogeneous coordinates) and 3 RGB colour vectors. The program packs all of these into 6 vec3 attributes and uses a shader to explode points into rectangles (geometry shader) and colour the butterfly appropriately (fragment shader). The full source code is here, including a colour index image of a butterfly I drew on paper and scanned in:
I didn't feel like wrapping it back around into a circle like Escher's original, maybe I'll try it another time. I think my more-symmetrical colouring is an improvement, but Escher's butterflies are much more beautifully drawn!