Preperiodic Mandelbrot set Newton basins
I previously wrote about Mandelbrot set Newton basins in the context of finding islands, whose nuclei are periodic points. A periodic point of a function g satisfies gp = g0, where p is called the period. For the Mandelbrot set the function is fc : z → z² + c. This post is about preperiodic points that satisfy gp+k = gk, where p is the period (still) and k is the called the preperiod.
Newton's method tries to find a root of a function h(x) = 0 by iterating x → x - h(x) / h'(x) where h' = dh/dx, namely the differential of h with respect to x. Here the quadratic function f in the Mandelbrot set is considered as a function of c, with f' = df/dc and we want to find a preperiodic c0 satisfying fc0p+k = fc0k.
Now, f and f' can be computed by recurrence relations:
Fc0 = 0
F'c0 = 0
Fcn+1 = (Fcn)² + c
F'cn+1 = 2 Fcn F'cn + 1
Applying Newton's method gives:
c → c - (Fcp+k - Fck) / (F'cp+k - F'ck)
But solving this isn't the whole story - it might converge to a preperiodic point with a preperiod less than k, say k'. (Even the target period p may be a multiple of the true period, say p'.) The next step is to find the true preperiod of the resulting c0, which can be done by finding the smallest k such that the Newton's method iteration starting with c0 still converges to c0 itself and not some other point.
Enough of how (for full details read the source linked below), here are some images, each with a certain fixed period and coloured according to the true preperiod of the root converged to at each pixel.
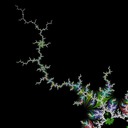
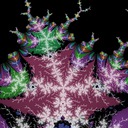
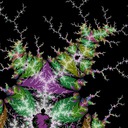
Image a shows the whole Mandelbrot set with some preperiodic basins of period 1 highlighted. You can see they surround some terminal and branch points, but not all. Images b and c show enlarged regions near the 1/3 and 2/5 bulbs. Image d starts to get interesting - this is zoomed in near the 1/3 child of the 1/2 bulb. Notice how only the outer filaments have basins attached. Compare with image e which increases the target period to 2: here the inner filaments have basins attached.
This leads me to conjecture that multiplicative tuning is at work: the inner filaments near a child atom will have preperiodic branch points that have a period a multiple of the parent atom's period, compared to the corresponding preperiodic branch points at the root. This seems to be supported by the remaining images: f, g, h with periods 1, 2, 3 highlighted near the period 3 island; i near a period 4 island with period 4 highlighted, and j near a period 5 island with period 5 highlighted. Note the inner filaments being highlighted when the periods match.