mathr / blog / #

The Mandelbrot is asymptotically self-similar about pre-periodic Misiurewicz points. The derivative of the cycle (with respect to \(z\)) can be used as a multiplier for seamlessly looping zoom animations. Here are some examples:

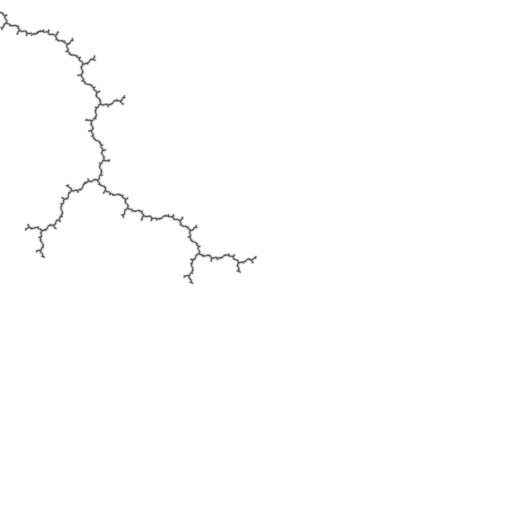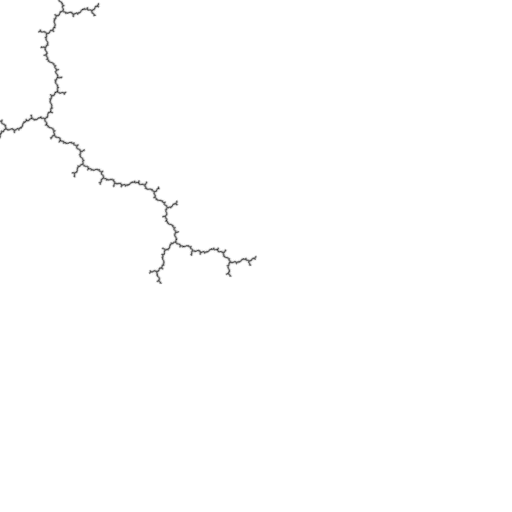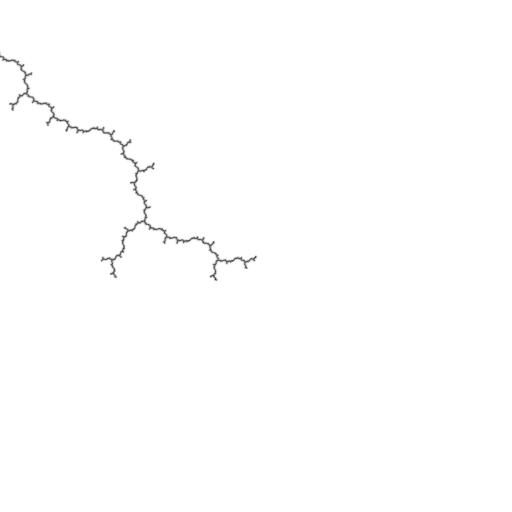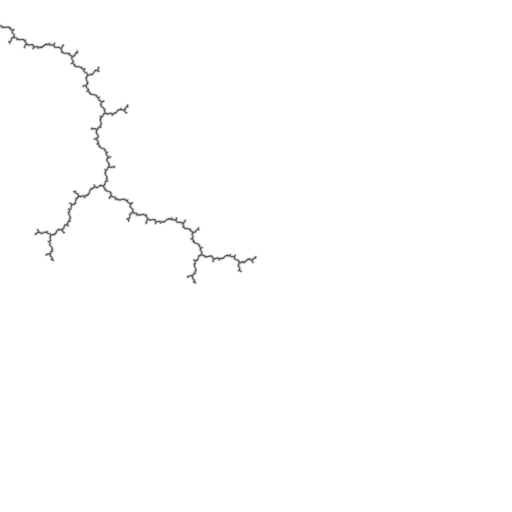
const dvec2 c0 = dvec2(-0.22815549365396179LF, 1.1151425080399373LF);
const int pre = 3;
const int per = 1;

const dvec2 c0 = dvec2(-0.10109636384562216LF, 0.9562865108091415LF);
const int pre = 4;
const int per = 3;

(The above example's Misiurewicz point has period 1, but using 3 here avoids rapid spinning.)

const dvec2 c0 = dvec2(-0.77568377LF, 0.13646737LF);
const int pre = 24;
const int per = 2;

Here is the rest of the code that made the images, it's for Fragmentarium with my (as yet unreleased, but coming soon) Complex.frag enhancements for dual-numbers and double-precision:

#version 400 core

#include "Complex.frag"
#include "Progressive2D.frag"

uniform float time;

// insert snippets from above in here to choose image

const double r0 = 0.00001LF;

vec3 color(vec2 p)
{
  // calculate multiplier for zoom
  dvec4 z = cVar(0.0LF);
  dvec4 c = cConst(c0);
  for (int i = 0; i < pre; ++i) z = cSqr(z) + c;
  z = cVar(cVar(z));
  for (int i = 0; i < per; ++i) z = cSqr(z) + c;
  dvec2 m = r0 * dvec2(cPow(vec2(cInverse(cDeriv(z))),
    mod(time, float(per)) / float(per)));
    
  const int maxiters = 1000;
  const double er2 = 1000.0LF;
  c = cVar(c0 + cMul(m, p));
  z = cConst(0.0LF);
  double pixelsize = cAbs(m) * double(length(vec4(dFdx(p), dFdy(p))));
  int i;
  for (i = 0; i < maxiters; ++i)
  {
    z = cSqr(z) + c;
    if (cNorm(z) > er2)
    {
      break;
    }
  }
  if (i == maxiters)
  {
    return vec3(1.0, 0.7, 0.0);
  }
  else
  {
    double de = 2.0 * cAbs(z) * double(log(float(cAbs(z)))) / cAbs(cDeriv(z));
    float grey = tanh(clamp( float(de/pixelsize), 0.0, 8.0 ));
    return vec3(grey);
  }
}