# Analytical Design
Using symbolic dynamics to design fractal artwork.
# 1 Beyond 23
Starting from the embedded Julia set with
angled internal address 1 2 3 1/8 23.
Morph to the period 49 = 2 * 23 + 3 node in the 1/2 wake.
Morph to the period 101 = 2 * 49 + 3 node in the 1/2 wake.
Repeat this process indefinitely.
# 1.1 Angled Internal Address
A small Haskell program to calculate the angled internal address of the nth item in the sequence, starting from period = 23 at n = 1:
import Data.List (intercalate)
address n
= ("1 2 3 1/8 " ++)
. intercalate " "
. map show
. take n
. iterate (\p -> 2 * p + 3)
$ 23
# 1.2 External Angle
These strings can be parsed and converted to pairs of external angles, which are conveniently expressed as periodic binary expansions:
import Mandelbrot.Prelude
angles
= both (drop 2 . init . plain . binary)
. addressAngles
. pAddress
. address -- defined above
both f (a, b) = (f a, f b)
Converting angled internal addresses to binary angles takes some time. Concatenating strings is much quicker. The next step is figuring out which strings to concatenate.
# 1.3 Pattern Analysis
Output the first few sets of angles:
import Control.Monad (forM_)
main = forM_ [1..5] $ \n -> do
let (lo, hi) = angles n
putStrLn (show n)
putStrLn ""
putStrLn lo
putStrLn ""
putStrLn hi
putStrLn ""
Which outputs
1
01101101101101101101110
01101101101101101110001
2
0110110110110110110111001101101101101101110001100
0110110110110110111000101101101101101101101110011
3
01101101101101101110001011011011011011011011100110110110110110110110111001101101101101101110001011100
01101101101101101110001011011011011011011011100110110110110110110110111001101101101101101110001100011
4
0110110110110110111000101101101101101101101110011011011011011011011011100110110110110110111000110001101101101101101101110001011011011011011011011100110110110110110110110111001101101101101101110001011011100
0110110110110110111000101101101101101101101110011011011011011011011011100110110110110110111000110001101101101101101101110001011011011011011011011100110110110110110110110111001101101101101101110001011100011
5
01101101101101101110001011011011011011011011100110110110110110110110111001101101101101101110001100011011011011011011011100010110110110110110110111001101101101101101101101110011011011011011011100010111000110110110110110110111000101101101101101101101110011011011011011011011011100110110110110110111000110001101101101101101101110001011011011011011011011100110110110110110110110111001101101101101101110001011011011100
01101101101101101110001011011011011011011011100110110110110110110110111001101101101101101110001100011011011011011011011100010110110110110110110111001101101101101101101101110011011011011011011100010111000110110110110110110111000101101101101101101101110011011011011011011011011100110110110110110111000110001101101101101101101110001011011011011011011011100110110110110110110110111001101101101101101110001011011100011
This is pretty opaque, but using the knowledge that (typically)
later bitstrings are made by copy-pasting earlier bitstrings,
and guided by the \p -> 2 * p + 3 pattern of the periods,
try to reformat it so any patterns are visible:
1
01101101101101101101110
01101101101101101110001
2
01101101101101101101110
01101101101101101110001 100
01101101101101101110001
01101101101101101101110 011
3
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 011 100
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 100 011
4
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 100 011
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 011 011 100
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 100 011
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 011 100 011
5
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 100 011
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 011 100 011
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 100 011
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 011 011 011 100
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 100 011
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 011 100 011
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 100 011
01101101101101101110001
01101101101101101101110 011
01101101101101101101110
01101101101101101110001 011 011 100 011
Labelling the lower angle at each stage o, and the upper i,
the first step from 1 to 2 is:
\(o, i) -> (o ++ i ++ "100", i ++ o ++ "011")
The second step from 2 to 3 is already trickier, but at least the upper part is the same:
\(o, i) -> (i ++ ?, i ++ o ++ "011")
The third step from 3 to 4 is confusing so far. Looking at the step from 4 to 5, the pattern seems to be revealed: it’s almost like
\(o, i) -> (i ++ o, i ++ i)
but each new block has “011” inserted 6 digits from the end.
# 1.4 Conjecture
The above leads to the following conjecture:
pattern (o, i) =
( i ++ replaceSuffix "011100" "011011100" o
, i ++ replaceSuffix "100011" "011100011" i
)
replaceSuffix needle replacement haystack
| needle == haystack = replacement
| otherwise = case haystack of
h:hs -> h : replaceSuffix needle replacement hs
[] -> error "replaceSuffix: not found"
where checking for the expected suffix is to help to detect if the conjecture is valid.
The expected suffix only exists from stage 3, so that’s the seed.
# 1.5 Theorem
Testing the conjecture:
main = forM_ [3 .. 7] $ \n -> do
print $ iterate pattern (angles 3) !! (n - 3) == angles n
prints True for these test cases so I suppose its ok (not proven rigourously though!). It takes over a minute to run in Hugs, the time being dominated by address to angle calculations.
# 1.6 Extrapolation
The list of periods ending at the first over 1M can be printed by:
main
= putStrLn
. unwords
. map show
. take 17
. iterate (\p -> 2 * p + 3)
$ 23
which outputs
23 49 101 205 413 829 1661 3325 6653 13309 26621 53245 106493 212989 425981 851965 1703933
And one of the final angles can be printed by:
main
= putStrLn
. (".(" ++) . (++ ")")
. fst
. (!! 14)
. iterate pattern
. angles
$ 3
which outputs a 1.7MB string that I won’t include here, taking about 5 seconds in Hugs (much faster than converting address to angles).
# 1.7 Ray Tracing
The whole point of this stuff with external angles, is that they can be converted to coordinates for rendering images, using an algorithm called “external ray tracing”.
The program m-exray-in-via (part of my mandelbrot-numerics library)
traces external rays using perturbation techniques,
given an angle (on stdin) and a list of periods (as arguments)
of references to use.
The period and coordinates of the references are output
(along with two more numbers which are for internal debugging).
Here I piped though ts, which shows that each next reference
takes over twice as long. As the 11th step took 23mins,
the 17th step is expected to finish in a few days.
Jul 17 09:03:35 23 -1.74633514734717192999519e+00 2.07795428756447413325244e-03 0.0000000000000000e+00 0.0000000000000000
Jul 17 09:03:35 49 -1.74633486482589918992643768e+00 2.07684336209284403849083121e-03 1.7463363836197453e+00 179.9318241090836587
Jul 17 09:03:35 101 -1.746336323507542951806601830636364626e+00 2.077698750144148599452026855476806781e-03 1.1462869069596916e-06 -75.7314866467596709
Jul 17 09:03:36 205 -1.74633633100972859200274231936097238667210e+00 2.07770993199709122129778689580850218177491e-03 1.6909881301069132e-06 149.6121394759637552
Jul 17 09:03:38 413 -1.74633633100731203448693541857192011832282528195609e+00 2.07770992931759947498951156281311613332803673420334e-03 1.3465386166404066e-08 123.8586514515695381
Jul 17 09:03:45 829 -1.746336331007312034486935402967007740930139175151113471916062817428e+00 2.077709929317599474989506042011876088075158436781760255391826095601e-03 3.6082442053908975e-12 -47.9535967875120835
Jul 17 09:04:15 1661 -1.7463363310073120344869354029670077409231543658125461180309896474285249339529727807454356605e+00 2.0777099293175994749895060420118760848491869012422276656716077111313848709361939567416133797e-03 1.6552719916623632e-26 -19.4830720472748943
Jul 17 09:05:52 3325 -1.74633633100731203448693540296700774092315436581254611803325193168381308728011150208513167019595429158355305443112947196533853088e+00 2.07770992931759947498950604201187608484918690124222766722007389279534979028185356123800225021156175232502789685337340415867851975e-03 7.6937932025918790e-39 -24.7901065222730735
Jul 17 09:10:06 6653 -1.746336331007312034486935402967007740923154365812546118033251931683813087280111502085627299341858766423513060798655737625169488900814755877361940049002481303016793848494744162753267047e+00 2.077709929317599474989506042011876084849186901242227667220073892795349790281853560896466147113669128422879380314191609810670105698882015552396775664490620081686570655143335730199976986e-03 2.7414736123992976e-57 145.6095220480795800
Jul 17 09:20:03 13309 -1.74633633100731203448693540296700774092315436581254611803325193168381308728011150208562729934185876642351306079865573762516948551841422971135489737098688353733425703865667227138991254140559019793350691207072113819940540511458099026453359117235390439801001721027451330201e+00 2.07770992931759947498950604201187608484918690124222766722007389279534979028185356089646614711366912842287938031419160981067058106210846403016855798078929551431193963843476051125938777415015216658903876498407877900737863618682598393346026300747387440414714831108853043638e-03 6.0190959453168176e-85 -145.4294253976338218
Jul 17 09:43:16 26621 -1.7463363310073120344869354029670077409231543658125461180332519316838130872801115020856272993418587664235130607986557376251694855184142297113548973709868835373342570386566722713899125414055900856695267201713924036710692220103507637521944471562516911831707895410112192365516663041743684904516658982814000368156021939494396953072509759875690029947902239064728734155917392297586463904695791943165224848e+00 2.0777099293175994749895060420118760848491869012422276672200738927953497902818535608964661471136691284228793803141916098106705810621084640301685579807892955143119396384347605112593877741501153889029566315408379148394711413737563464890849555801807507921137751989616893605705660059914141883303008691430816086889542375429088277134971473479217183850413207936618885384522404550042749231947447586323457373e-03 3.4156410110647738e-126 7.9999640067258766
Unfortunately external ray tracing is an inherently serial algorithm, so multicore CPU or GPU are no benefit.
# 1.8 Viewport
The coordinates are only the center of the view. To render an image, the size (zoom depth) is also needed.
From prior experience, the zoom depth of an embedded Julia morph
is often related to the atom domain size by an exponent of 9/8
and a constant scale factor (typically in the range 1 to 100).
For example, the period 3325 nucleus in the output above,
fed into m-domain-size from mandelbrot-numerics, arbitrarily using
1000 bits of precision
(too low will cause errors,
too high will waste computation time), gives
1.0081875719169438e-75
Using Hugs as a calculator, noting that zoom = 4 / size
(some software uses size, some uses zoom):
> 4 / (10 * 1.0081875719169438e-75 ** 1.125)
9.39887739382545e+83
# 1.9 Image
Feeding the coordinates and zoom depth to Fraktaler-3 gives this image of the period 3325 stage:
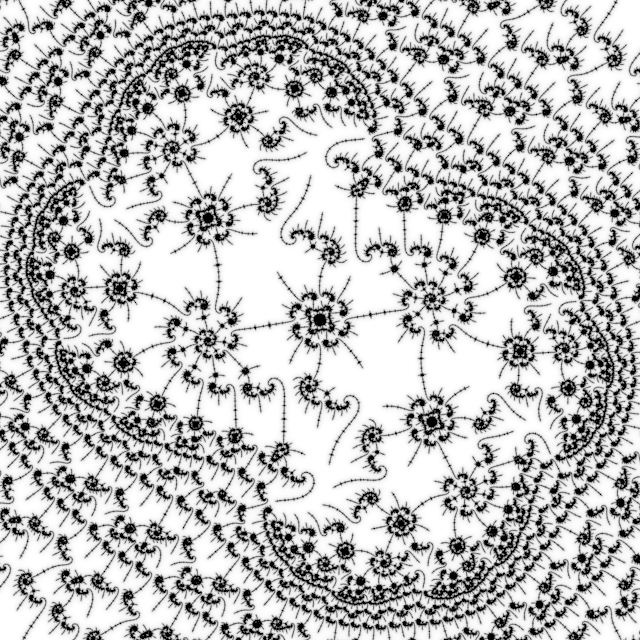
Parameters: F3 TOML
The period 1.7M image (when the ray tracing finishes…) will be added to my Millionaires page.
# 2 Right 23
Doing the same as Beyond 23,
but with ìntercalate " 1/3 "
instead of intercalate " "
gives a simpler pattern:
1
01101101101101101101110
01101101101101101110001
2
01101101101101101101110
01101101101101101101110 100
01101101101101101101110
01101101101101101110001 011
3
01101101101101101101110
01101101101101101101110 100
01101101101101101101110
01101101101101101101110 100 100
01101101101101101101110
01101101101101101101110 100
01101101101101101101110
01101101101101101110001 011 011
4
01101101101101101101110
01101101101101101101110 100
01101101101101101101110
01101101101101101101110 100 100
01101101101101101101110
01101101101101101101110 100
01101101101101101101110
01101101101101101101110 100 100 100
01101101101101101101110
01101101101101101101110 100
01101101101101101101110
01101101101101101101110 100 100
01101101101101101101110
01101101101101101101110 100
01101101101101101101110
01101101101101101110001 011 011 011
That is:
pattern (o, i) =
( o ++ o ++ "100"
, o ++ i ++ "011"
)
Tracing rays gives:
Jul 17 12:02:50 23 -1.74633514734717192999519e+00 2.07795428756447413325244e-03 0.0000000000000000e+00 0.0000000000000000
Jul 17 12:02:50 49 -1.74633548145057916309793739e+00 2.07914200586261670841929230e-03 1.7463363836197453e+00 179.9318241090836587
Jul 17 12:02:50 101 -1.74633547654049046285826942621248e+00 2.07914062238913243500916524343038e-03 1.2338151573341379e-06 105.7112143536725770
Jul 17 12:02:51 205 -1.746335476541127790415919525459487428586e+00 2.079140623084958192471124461783761576532e-03 5.1012714028866257e-09 -15.7357876035526123
Jul 17 12:02:53 413 -1.74633547654112779262053742329718025298547262977044e+00 2.07914062308495897791130824388486742822322555623627e-03 9.4358884080289435e-13 132.4874973028281012
Jul 17 12:03:00 829 -1.7463354765411277926205374142161053858041595736529061182109921309366e+00 2.0791406230849589779113109568610982917092689841778834669666415868234e-03 2.3403538958383940e-18 160.3905196109885694
Jul 17 12:03:30 1661 -1.74633547654112779262053741421610538580179078976421433044236742556582718071020357279312111983e+00 2.07914062308495897791131095686109829080307837412287377319236163733274019073942514209017327317e-03 9.4776664201997714e-27 16.6335451044815726
Jul 17 12:05:07 3325 -1.7463354765411277926205374142161053858017907897642143304422898565104236627345880158560056740211239262554101509467874550219165330426e+00 2.0791406230849589779113109568610982908030783741228737728402854243538020678750404853300909892074335568290309982799825737920118083704e-03 2.5362015955120088e-39 -20.9346118819963777
Jul 17 12:09:15 6653 -1.746335476541127792620537414216105385801790789764214330442289856510423662734588015855987027871163667573832967002426725605666001851805343180940944269010997417634380981513578297317034415088e+00 2.079140623084958977911310956861098290803078374122873772840285424353802067875040485336082803222190035928481963222673695603777482276706940346699339043684873091097262891413391475227844213305e-03 3.6051992746835041e-58 -77.5751527593522321
Jul 17 12:18:53 13309 -1.7463354765411277926205374142161053858017907897642143304422898565104236627345880158559870278711636675738329670024267256056660018443489946553313404559202268490628017620503563634095506937110192797415604053048668480558653492508830444787389840891221817510279997087232310591165e+00 2.0791406230849589779113109568610982908030783741228737728402854243538020678750404853360828032221900359284819632226736956037774797544371833280730260354639334453740478446865805441311732487975533775486416164613046386955993459028886847904321339326352283211443061129550601091279e-03 1.9585217474613015e-86 17.8144568675296505
Jul 17 12:41:31 26621 -1.74633547654112779262053741421610538580179078976421433044228985651042366273458801585598702787116366757383296700242672560566600184434899465533134045592022684906280176205035636340955069371101928032055610539385971916785767049203379135087882280443738417754349637444493386226357981870029963204858519974407442209622983671782848395008727873317324880873373328310837905044901729078734254174186460862945983584e+00 2.07914062308495897791131095686109829080307837412287377284028542435380206787504048533608280322219003592848196322267369560377747975443718332807302603546393344537404784468658054413117324879755529578348024287636934712042391518848197455735625663389463343081078768622277891312183241452328711204654041476011886582755781572600252658299028251613679662119426375645281472290072066004394302991612379467701189962e-03 7.8714025473565586e-129 -18.6892099130054960
The period 3325 image is then:
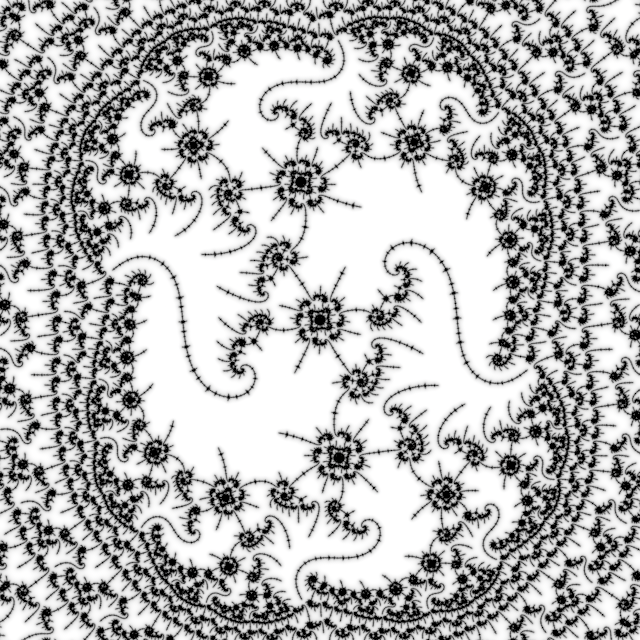
Parameters: F3 TOML
The atom domain size linear scale factor is 12 instead of 10.
# 3 Left 23
Doing the same as Beyond 23,
but with ìntercalate " 2/3 "
instead of intercalate " "
gives another simple pattern:
pattern (o, i) =
( i ++ o ++ "100"
, i ++ i ++ "011"
)
However, trying to trace the rays failed quite early:
Jul 17 12:35:39 23 -1.74633514734717192999519e+00 2.07795428756447413325244e-03 0.0000000000000000e+00 0.0000000000000000
Jul 17 12:35:39 49 -1.74633402413115550228934451e+00 2.07826598696372738135560175e-03 1.7463363836197453e+00 179.9318241090836587
Jul 17 12:35:40 101 -1.7463348724496896286564354786783866e+00 2.0768655013555391353975085414886591e-03 1.1656632168231784e-06 15.5096639188026663
Jul 17 12:35:40 205 -1.74633486339842676418514603941107177368347498e+00 2.07684837296023536872562393360703779267932562e-03 1.6373772546620737e-06 -121.2046184400369639
m-exray-in-via: error: nucleus failed at period = 413 (depth = 1735)
I worked around it by adding 8 to the target dwell (equivalent to adding 24 to depth), which is when to stop tracing the ray and switch to Newton’s root finding method to locate the nucleus.
Not entirely satisfied, but it let me get this period 3325 image:
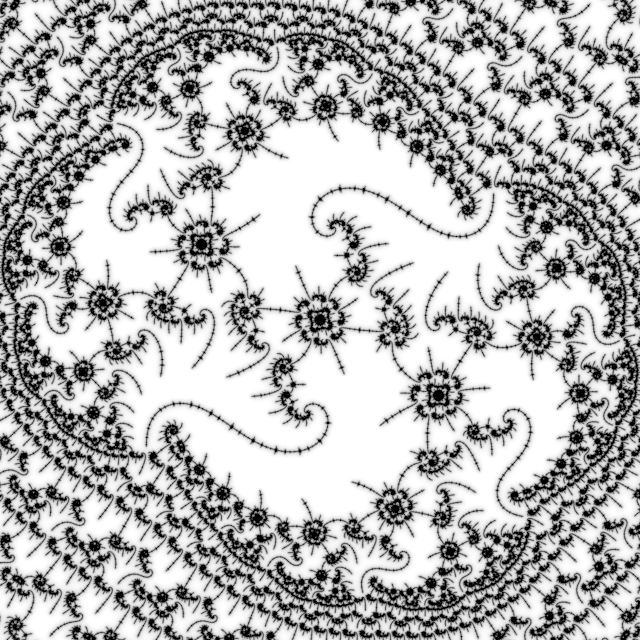
Parameters: F3 TOML
The atom domain size linear scale factor is 12 instead of 10.
I struggle to see the difference to the Right image, perhaps I will try orienting them the same, by using the next nucleus in the series as a “handle”. Perhaps the differences are only visible in the rings of decorations, and not the central feature, so zooming out a little is another idea to try.
# 4 Before 23
Doing the same as Beyond 23, but going to the node opposite the 1/2 wake, needs some care as the angled internal addresses are no longer so simple.
-
use a graphical explorer to find the nodes
-
trace their rays outwards to find their external angles
-
reverse engineer the pattern of external angles
The pattern turned out to be another simple one:
pattern (o, i) =
( o ++ o ++ "011"
, i ++ i ++ "100"
)
starting from the period 23 island.
Period 3325 image:

Parameters: F3 TOML
The atom domain size linear scale factor is 12 instead of 10.
The angled internal addresses corresponding to the nodes are:
1 2 3 1/8 23
1 2 3 1/8 24 25 26 47 48 49
1 2 3 1/8 24 25 26 47 48 50 51 52 73 74 75 96 97 99 100 101
1 2 3 1/8 24 25 26 47 48 50 51 52 73 74 75 96 97 99 100 102
103 104 125 126 127 148 149 151 152 153 174 175 176 197 198 200 201 203 204 205
1 2 3 1/8 24 25 26 47 48 50 51 52 73 74 75 96 97 99 100 102
103 104 125 126 127 148 149 151 152 153 174 175 176 197 198 200 201 203 204 206
207 208 229 230 231 252 253 255 256 257 278 279 280 301 302 304 305 307 308 309
330 331 332 353 354 356 357 358 379 380 381 402 403 405 406 408 409 411 412 413
What a mess! No hope of reverse engineering that.
# 5 Inside 23
Exploring graphically in m-perturbator-gtk
(in the same 1 2 3 1/8 23 embedded Julia set)
and tracing some rays gave the following pattern
of external angles:
import System.IO (hPutStrLn, stderr)
periods = iterate (\p -> 2 * p + 23 + 1) (23 + 23 + 1)
o23 = "01101101101101101101110"
i23 = "01101101101101101110001"
seed =
( o23 ++ i23 ++ "1"
, i23 ++ o23 ++ "0"
)
pattern (o, i) =
( o ++ i ++ i23 ++ "1"
, i ++ o ++ o23 ++ "0"
)
main = do
hPutStrLn stderr . unwords . map show . take 10 $ periods
putStrLn $ ".(" ++ (fst $ iterate pattern seed !! 10) ++ ")"
The period 4520 image looks like:
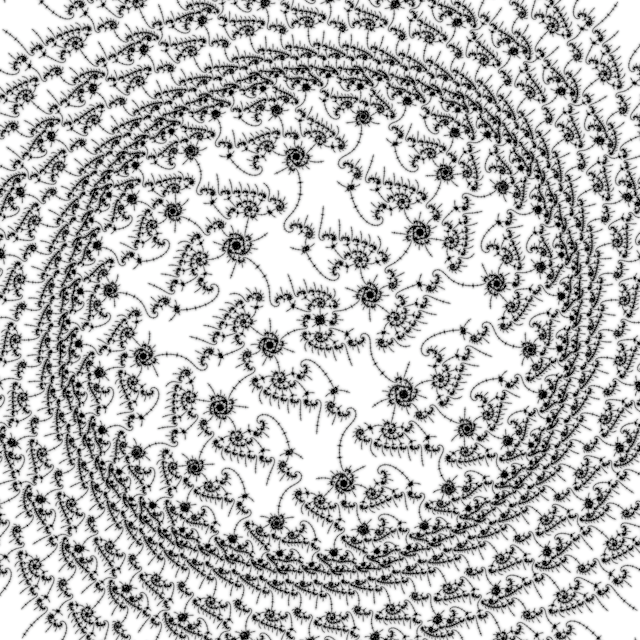
Parameters: F3 TOML
Exploration: MP TOML
# 5.1 Elephant Balls
As above, but with denominator in 1/8 varied from 2 to 17:
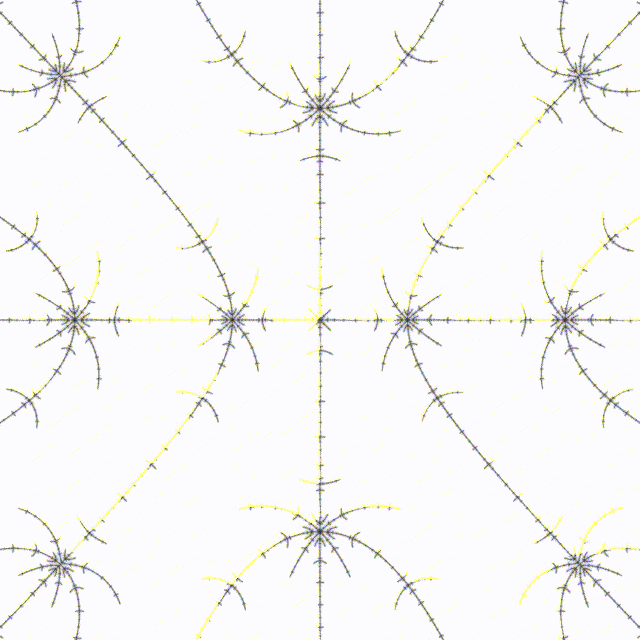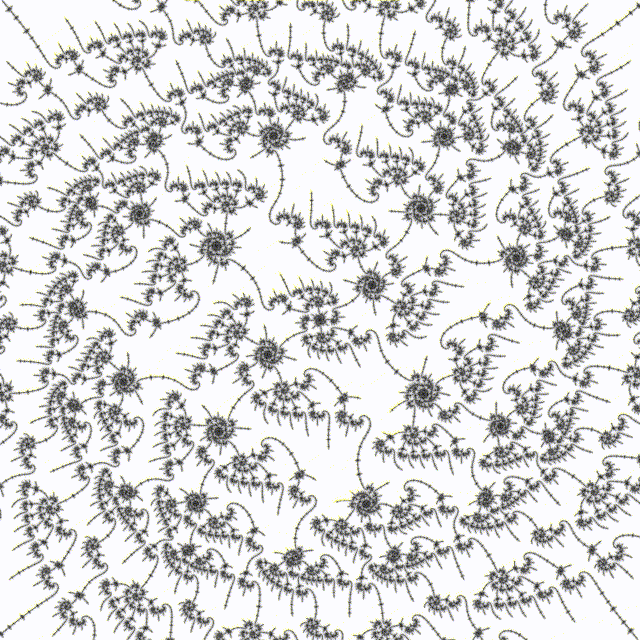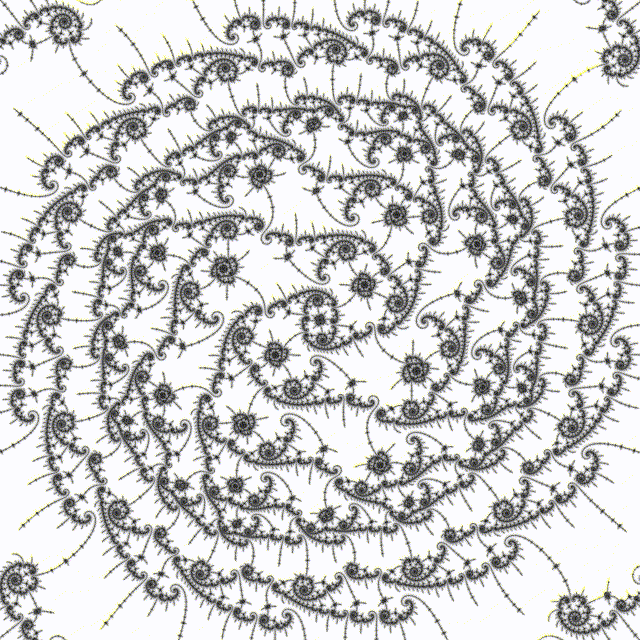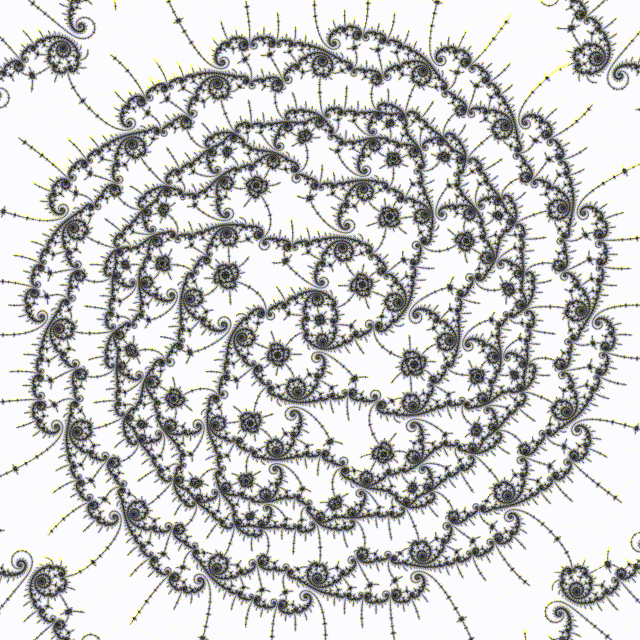
Haskell program to generate variations
of a given depth d and denominator n,
file eb.hs:
import Mandelbrot.Prelude (plain, binary, addressAngles, pAddress)
import System.Environment (getArgs)
import System.IO (hPutStrLn, stderr)
periods n = m : iterate (\p -> 2 * p + m + 1) (2 * m + 1)
where
m = 3 * n - 1
angles n
= both (init . drop 2 . plain . binary)
. addressAngles
. pAddress
$ "1 2 3 1/" ++ show n ++ " " ++ show (3 * n - 1)
both f (a, b) = (f a, f b)
seed (o, i) =
( o ++ i ++ "1"
, i ++ o ++ "0"
)
pattern (oo, ii) (o, i) =
( o ++ i ++ ii ++ "1"
, i ++ o ++ oo ++ "0"
)
main = do
[sd, sn, mode] <- getArgs
d <- readIO sd
n <- readIO sn
case mode of
"p" -> putStrLn . unwords . map show . take d . periods $ n
"a" -> let oi = angles n
in putStrLn $ ".(" ++ fst (iterate (pattern oi) (seed oi) !! (d - 2)) ++ ")"
Script to render animation (file eb.sh):
#!/bin/bash
for p in $(seq 2 17)
do
mandelbrot-prelude/runhugs.sh eb.hs 7 $p a |
m-exray-in-via $(mandelbrot-prelude/runhugs.sh eb.hs 7 $p p) |
tee eb-$p.txt
cat eb-$p.txt |
tail -n 2 |
(
read q cre cim junk
read q dre dim junk
ghc -e "let x = fromRational (($dre) - ($cre)) ; y = fromRational (($dim) - ($cim)) in putStrLn (\"location.real = \\\"$cre\\\"\\nlocation.imag = \\\"$cim\\\"\\nlocation.zoom = \\\"\" ++ show (0.02 * 4 / sqrt (x^2 + y^2)) ++ \"\\\"\\ntransform.rotate = \" ++ show (360 / (2 * pi) * atan2 y x) ++ \"\\nrender.filename = \\\"eb-$p\\\"\")"
) |
tee eb-$p.f3.toml
fraktaler-3-3~pre -P -b eb.f3.toml eb-$p.f3.toml
done
ffmpeg -r 3 -i eb-%d.png -y eb.gif
Common F3 TOML for rendering setup (file eb.f3.toml):
bailout.iterations = 100100
bailout.maximum_reference_iterations = 100100
bailout.maximum_perturb_iterations = 4096
bailout.maximum_bla_steps = 4096
image.width = 640
image.height = 640
image.subframes = 16
render.save_png = true
[colour]
uniforms = []
shader = """
vec3 colour(void)
{
const float gamma = 1.0;
vec2 DE = getDE();
float val = tanh(clamp(length(DE), 0.0, 4.0));
return vec3(pow(val, 1.0 / gamma));
}
\
"""
# 6 Inside 23 3/8
Replacing 1/8 with 3/8 in the initial seed gives a variation:

Parameters: F3 TOML
# 7 Line 23
Exploring extending a line in the 1/2 wake, this pattern works by splitting the digit blocks in half and swapping them over.
import System.IO (hPutStrLn, stderr)
o23 = "01101101101101101101110"
i23 = "01101101101101101110001"
seed =
( o23 ++ i23 ++ "10" ++ i23 ++ i23 ++ "10"
, i23 ++ o23 ++ "01" ++ o23 ++ o23 ++ "01"
)
pattern (o, i) =
( o ++ i1 ++ o2
, i ++ o1 ++ i2
)
where
(o1, o2) = split o
(i1, i2) = split i
split xs = half xs xs
where
half (x:xs) (_:_:ys) = first (x:) (half xs ys)
half xs [] = ([], xs)
half _ _ = error "split: length is odd"
first f ~(xs, ys) = (f xs, ys)
periods = 23 : iterate (* 2) 48
main = do
hPutStrLn stderr . unwords . map show . take 17 $ periods
putStrLn $ ".(" ++ fst (iterate pattern seed !! 14) ++ ")"
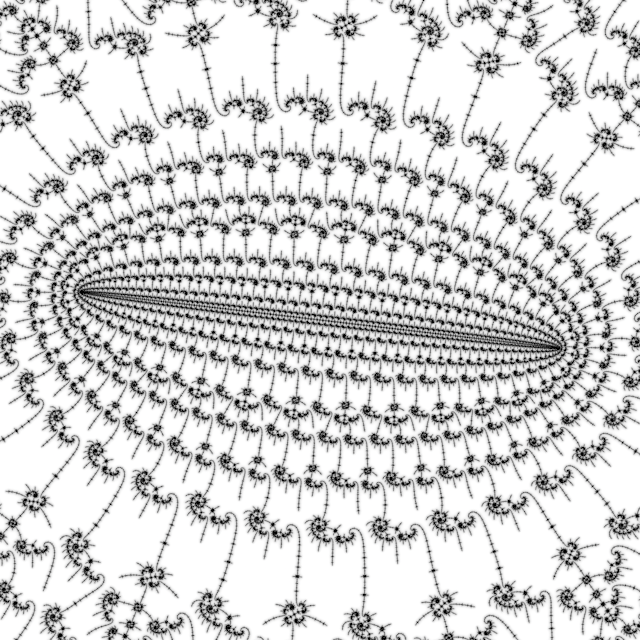
Parameters: F3 TOML
Exploration: MP TOML
# 7.1 Elephant Lines
As above, but with denominator in 1/8 varied from 2 to 17:

Haskell program to generate variations
of a given depth d and denominator n,
file el.hs:
import Mandelbrot.Prelude (plain, binary, addressAngles, pAddress)
import System.Environment (getArgs)
periods n = (3 * n - 1) : iterate (* 2) ((3 * n - 1) * 2 + 2)
angles n
= both (init . drop 2 . plain . binary)
. addressAngles
. pAddress
$ "1 2 3 1/" ++ show n ++ " " ++ show (3 * n - 1)
both f (a, b) = (f a, f b)
seed (o, i) =
( o ++ i ++ "10" ++ i ++ i ++ "10"
, i ++ o ++ "01" ++ o ++ o ++ "01"
)
pattern (o, i) =
( o ++ i1 ++ o2
, i ++ o1 ++ i2
)
where
(o1, o2) = split o
(i1, i2) = split i
split xs = half xs xs
where
half (x:xs) (_:_:ys) = first (x:) (half xs ys)
half xs [] = ([], xs)
half _ _ = error "split: length is odd"
first f ~(xs, ys) = (f xs, ys)
main = do
[sd, sn, mode] <- getArgs
d <- readIO sd
n <- readIO sn
case mode of
"p" -> putStrLn . unwords . map show . take d . periods $ n
"a" -> putStrLn $ ".(" ++ fst (iterate pattern (seed (angles n)) !! (d - 3)) ++ ")"
Script to render animation (file el.sh):
#!/bin/bash
for p in $(seq 2 17)
do
mandelbrot-prelude/runhugs.sh el.hs 8 $p a |
m-exray-in-via $(mandelbrot-prelude/runhugs.sh el.hs 8 $p p) |
tee el-$p.txt
cat el-$p.txt |
tail -n 2 |
(
read q cre cim junk
read q dre dim junk
ghc -e "let x = fromRational (($dre) - ($cre)) ; y = fromRational (($dim) - ($cim)) in putStrLn (\"location.real = \\\"$cre\\\"\\nlocation.imag = \\\"$cim\\\"\\nlocation.zoom = \\\"\" ++ show (0.5 * 4 / sqrt (x^2 + y^2)) ++ \"\\\"\\ntransform.rotate = \" ++ show (360 / (2 * pi) * atan2 y x) ++ \"\\nrender.filename = \\\"el-$p\\\"\")"
) |
tee el-$p.f3.toml
fraktaler-3-3~pre -P -b el.f3.toml el-$p.f3.toml
done
ffmpeg -r 3 -i el-%d.png el.gif
Common F3 TOML for rendering setup (file el.f3.toml):
bailout.iterations = 100100
bailout.maximum_reference_iterations = 100100
bailout.maximum_perturb_iterations = 4096
bailout.maximum_bla_steps = 4096
image.width = 640
image.height = 360
image.subframes = 16
render.save_png = true
[colour]
uniforms = []
shader = """
vec3 colour(void)
{
const float gamma = 1.0;
vec2 DE = getDE();
float val = tanh(clamp(length(DE), 0.0, 4.0));
return vec3(pow(val, 1.0 / gamma));
}
\
"""