# Misiurewicz Domains

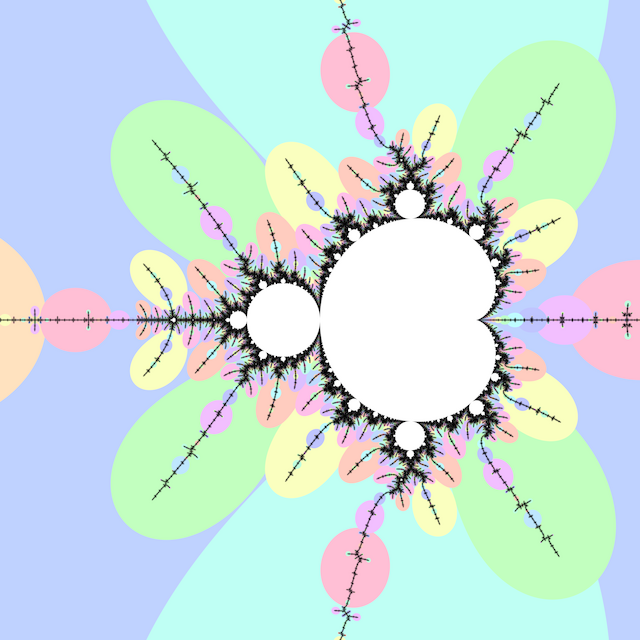
Preperiodic points in the Mandelbrot set are called Misiurewicz points, and they have repelling orbits (periodic hyperbolic components have attracting orbits). Atom domains show the period with the preperiod fixed at \(0\), while for Misiurewicz domains show the preperiod with the period fixed.

Misiurewicz domains (2015) defines the Misiurewicz domain for period \(p \ge 1\) as the index \(q\) at which \(\left|z_{p + q} - z_q\right|\) is minimized. Misiurewicz domains surround Misiurewicz points whose period divides \(p\), and are much larger than a single point, which makes makes them useful for finding Misiurewicz points.

#include <complex.h>

int m_misiurewicz_domains
    (int N, int p, double _Complex c)
{
    int q = 0;
    double _Complex z = c;
    double _Complex zp = c;
    double mq = 1.0 / 0.0;
    for (int n = 0; n < p; ++n)
        z = z * z + c;
    for (int n = 0; n < N - p; ++n)
    {
        double zq = cabs(z - zp);
        if (zq < mq)
        {
            mq = zq;
            q = n;
        }
        z = z * z + c;
        zp = zp * zp + c;
    }
    return q;
}