mathr / blog / #

Atom domains in the Mandelbrot set are defined as the index \(p \ge 1\) at which \(|z_p|\) is minimized during iteration of \(z_0 = 0\) and \(z_{n+1} = z_n^2 + c\). Atom domains surround hyperbolic components of the same period, and are generally much larger than the components themselves, which makes them useful for finding components.

I was thinking that something similar might be possible for the preperiodic case. Preperiodic points in the Mandelbrot set are called Misiurewicz points, and they have repelling orbits (periodic hyperbolic components have attracting orbits). Atom domains show the period with the preperiod fixed at 0, while for Misiurewicz domains I thought it would be more useful to fix the period and show the preperiod.

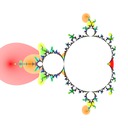
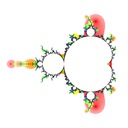
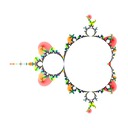
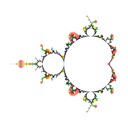
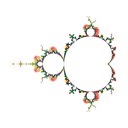
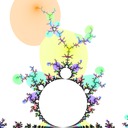
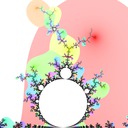
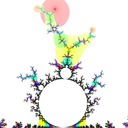
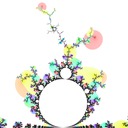
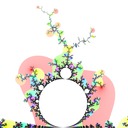
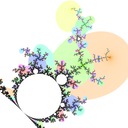
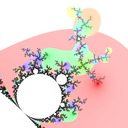
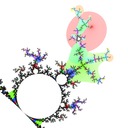
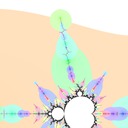
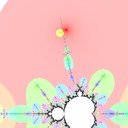
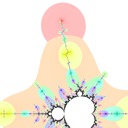
I defined the Misiurewicz domain for period \(p \ge 1\) as the index \(q\) at which \(|z_{p+q} - z_q|\) is minimized. It turns out that Misiurewicz domains surround Misiurewicz points whose period divides \(p\), and are much larger than a single point, which makes makes them useful for finding Misiurewicz points. Here are some pictures for different views and periods:

And here's the relevant part of the inner loop (ignoring derivatives for distance estimation, escape tests, interior checking, etc):

complex double z = c;
complex double zp = c;
int q = 0;
double mq2 = 1.0 / 0.0;
for (int n = 0; n < p; ++n) {
  z = z * z + c;
}
for (int n = 0; n < maxiters - p; ++n) {
  double q2 = cabs2(z - zp);
  if (q2 < mq2) {
    mq2 = q2;
    q = n;
  }
  z = z * z + c;
  zp = zp * zp + c;
}
plot(c, hsv2rgb((q - 1) * hue, (q > 0) * sat, val));

You can download the full Misiurewicz domains C99 source code, which depends on my work-in-progress not-even-alpha-yet mandelbrot mandelbrot libraries mandelbrot-numerics (git HEAD at 92ccbf7fbc678f97ba2d8d370eb6859531697da0) and mandelbrot-graphics (git HEAD at fdb4c52e982a9c79250c7100ffa6243997f3ca68).