# Ten Dust Tree
Taper is an online literary journal for computational poetry and literary art published twice yearly by Bad Quarto.
My piece Ten Dust Tree is published in Taper#10.
View page source in browser to see the code and artist comment.
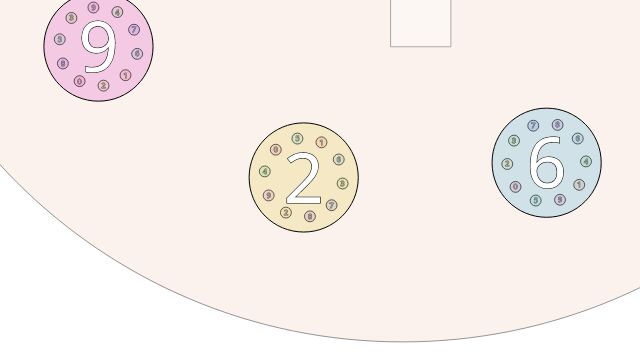
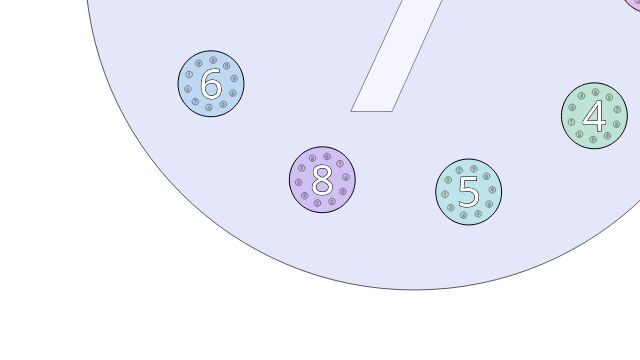
# 1 Screenshots
For archival purposes, static images (click to enlarge):
# 2 Videos
For archival purposes, a static video excerpt (11MB):
HD version (69MB).
# 3 How It Works
# 3.1 Counting
Champernowne’s constant \(C_{10}\) is made by concatenating all the natural numbers in base 10. It starts \[0.1234567891011121314151617181920212223\ldots.\] To construct it, we can use two nested loops, one for the natural number, and one for its digit position:
for (int number = 0; ; ++number)
{
char string[100];
snprintf(string, sizeof(string), "%d", number);
int digits = strlen(string);
for (int position = 0; position < digits; ++position)
{
int digit = string[position] - '0';
// do something with digit
}
}
However, we don’t have an outer loop, because the animation is driven by frame events, so the control is inverted:
var number = 0, digits = 1, position = 0;
function nextDigit()
{
var string = "" + number;
var digit = parseInt(string.substring(position, position + 1));
if (++position == digits)
{
position = 0;
if (++number == Math.pow(10, digits))
{
++digits;
}
}
return digit;
}
In the size-coded version, this is function n().
# 3.2 Shuffle
To randomize the order of the digits at each level of the fractal, we can shuffle the array. This works by swapping each item with a random choice of the items remaining (including possibly the item itself), ordered from the back of the array for numerical convenience.
function shuffle(array)
{
for (var i = array.length - 1; i > 0; --i)
{
var j = Math.floor(Math.random() * (i + 1));
[array[i], array[j]] = [array[j], array[i]];
}
return array;
}
In the size-coded version, this is function H().
# 3.3 Tree Building
The fractal is structured in a tree
with a digit at each node
surrounded by 10 more nodes.
The permutation is the inverse mapping of digits vs positions,
but since it’s randomly chosen it doesn’t matter.
The child at index n in the array corresponds to digit n.
function buildTree(depth, x, y)
{
var offset = Math.random();
var permutation = shuffle([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]),;
var radius = Math.pow(10, depth + 1);
var tree = [];
for (var digit = 0; digit < 10; ++digit)
{
var angle = (offset + permutation[digit]) * Math.PI / 10;
var u = x + radius * Math.cos(angle);
var v = y + radius * Math.sin(angle);
tree.push(
{ x: u
, y: v
, children: depth > 0 ? buildTree(depth - 1, u, v) : []
}
);
}
return children;
}
In the size-coded version, this is function B()
# 3.4 Tree Growing
The fractal is infinite, but the computer is not, so the tree is only built to a certain depth (the deeper levels may be too small to see in any case). When zooming in, the finite depth would become apparent, so the tree can be grown as necessary, adding another layer at the deepest level.
Some of the nodes may be outside the visible area, and as the zoom animation is constantly inwards, they will never be visible again. Therefore skipping the growing of these tree nodes will save both processing time and space.
var canvasElement = document.getElementById("c");
function visible(x, y)
{
var w = canvasElement.width;
var h = canvasElement.height;
return 4 * (x * x + y * y) < w * w + h * h;
}
In the size-coded version, this is function V().
function growTree(tree, x, y)
{
if (tree.length == 0 && visible(x,y))
{
return buldTree(0, x, y);
}
else
{
for (var digit = 0; digit < tree.length; ++digit)
{
var child = tree[digit];
child.x *= 10;
child.y *= 10;
child.children = growTree(child.children, child.x, child.y);
}
}
return tree;
}
In the size-coded version, this is function U()
# 3.5 Animation
Animation is controlled by a time variable,
which is incremented each frame.
The speed increases so that
each number-group of digits takes about the same amount of wall-clock time.
The time variable is a logical time in \([0..1)\), not wall-clock time,
and controls the zooming (which is exponential to give a continuous flow).
When time passes 1, it wraps back to 0 and grows the tree,
discarding the outermost layer.
The path of nextDigit()s is used to center the zooming
on the right place before it is really visible.
This is all hardcoded to a tree with 3 layers, which corresponds to a zoom factor of 1000. As most screens are about 1000 pixels, this makes the smallest details about 1 pixel, going smaller is probably not necessary.
var speed = 1;
var time = 0; // animated in [0..1)
var zoom = Math.pow(10, time);
var path = [nextDigit(), nextDigit(), nextDigit()];
var previousTime = null;
function animate(currentTime)
{
var dt = previousTime == null ? 0 : Math.min(1000, speed * (currentTime - previousTime));
previousTime = currentTime;
// accelerate based on digit count
// default speed takes ~2 seconds to count each number
var speedMultiplier = Math.log(number) / Math.log(10);
time += dt / 2000 * speedMultiplier;
zoom = Math.pow(10, time);
while (time > 1)
{
// add a new layer to the tree
time -= 1;
zoom /= 10;
tree = growTree(tree, 0, 0)[path[0]].children;
path[0] = path[1];
path[1] = path[2];
path[2] = nextDigit();
}
context.clearRect(0, 0, canvasElement.width, canvasElement.height);
// smoothly center on the end of the path
var a = tree[path[0]].children[path[1]];
var b = a.children[path[2]];
var tween = 0.5 - 0.5 * Math.cos(Math.PI * time);
tween *= tween;
var dx = -(a.x + tween * (b.x - a.x));
var dy = -(a.y + tween * (b.y - a.y));
// draw the tree (side-effect: updates position)
drawTree(tree, 3, dx, dy);
window.requestAnimationFrame(animate);
}
animate();
In the size-coded version, this is function T().
# 3.6 Drawing
Drawing proceeds recursively. Colour circles according to digit value. Measure the text to center it vertically.
var context = canvasElement.getContext("2d");
context.textAlign = "center";
function drawTree(tree, depth, dx, dy)
{
// draw nodes
for (var digit = 0; digit < tree.length; ++digit)
{
// side-effect: update position
tree[digit].x += dx;
tree[digit].y += dy;
// measure text
var string = "" + digit;
var fontSize = Math.pow(10, depth + time - 0.75);
context.font = "" + fontSize + "px sans-serif";
var metrics = context.measureText(string);
var offset = (metrics.actualBoundingBoxAscent - metrics.actualBoundingBoxDescent) / 2;
// transform to screen coordinates
var X = zoom * tree[digit].x + canvasElement.width / 2;
var Y = zoom * tree[digit].y + canvasElement.height / 2;
// fade out shallowest layer, fade in deepest layer
context.globalAlpha = depth == 3 ? 1 - time : depth == 1 ? t : 1;
// draw circle
context.fillStyle = "hsla(" + (36 * digit - 18) + ",66%,50%,0.2)";
context.strokeStyle = "#000";
context.beginPath();
context.arc(X, Y, 1.25 * 5/9 * Math.pow(10, depth + time - 0.7), 0, 2 * Math.PI, false);
context.fill();
context.stroke();
// draw text
context.fillStyle = "#fff";
context.strokeStyle = "#000";
context.beginPath();
context.strokeText(string, X, Y + offset);
context.fillText(string, X, Y + offset);
}
// draw children
for (var digit = 0; digit < tree.length; ++digit)
{
drawTree(tree[digit].children, depth - 1, dx, dy);
}
}
In the size-coded version this is function D().
# 3.7 Window Size
Resize the canvas to fill the window.
function handleResize()
{
canvasElement.style.width = "100%";
canvasElement.style.height = "100vh";
canvasElement.width = canvasElement.offsetWidth;
canvasElement.height = canvasElement.offsetHeight;
}
handleResize();
window.addEventListener("resize", handleResize);
In the size-coded version this is function Z().
# 3.8 Varispeed
An enhancement suggested by the reviewers on the editorial team, but not incorporated in the published version.
Speed can be changed with the #hash portion of the URL.
#100 is original speed (100%), #50 is half speed, #200 is double speed.
Be careful with #10000000000 in case you are sensitive to stroboscopic images.
It can be changed while the code is running,
so you don’t need to restart from the beginning.
window.onhashchange = (event) =>
{
try
{
speed = parseFloat(location.hash.substring(1)) / 100;
}
catch (error)
{
// ignore errors
}
// ignore non-positive values (including not-numbers)
speed = speed > 0 ? speed : 1;
};
window.onhashchange();
# 4 Exercises
-
Generalize to base B where B is not necessarily 10.
-
Generalize to tree depth D where D is not necessarily 3 (for 8K screens, maybe).
-
Use Roman numerals instead of base B expansions. The path would start \[IIIIIIIVVVIVIIVIIIXXXIXIIXII\ldots.\]
-
Allow starting from an arbitrary place in the path instead of the beginning.
-
Bugfix: correctly handle integers larger than 1022 (or earlier, if
Math.pow(10, n)is inaccurate).