# z→z²+cz⁵

# 1 Critical Points

\[f_c'(z) = 2 z + 5 c z^4 = 0\]

has 4 solutions

\[z_0 = 0 \\ z_0 = \sqrt[3]{-\frac{2}{5c}}\]

which is where iteration should start from to determine the number of components that the filled-in Julia set has (1 if all critical points remain bounded, infinitely many if a critical point escapes to infinity).

\(z_0 = 0\) implies \(z_n = 0\) for all \(n \ge 0\), which is not interesting.

# 2 Boundedness

Suppose \(|z_n| < r\). If that implies \(|z_{n+1}| < r\), then \(|z_m| < r\) for all \(n > m\) (by induction).

We want \[|z_{n+1}| = |z_{n}^2 + c z_{n}^5| < |z_{n}| + |c| |z_n|^5 < r^2 + |c| r^5 < r\] whence \[|c| < \frac{1 - r}{r^4}\]

Suppose \[|z_0| = \sqrt[3]{\frac{2}{5|c|}} < r\] whence \[\frac{2}{5r^3} < |c|\]

Maximizing \(r\) such that \[\frac{2}{5r^3} < |c| < \frac{1 - r}{r^4}\] gives \[r < \frac{5}{7},\] that is, if \(|z_{n}| < \frac{5}{7}\) for any \(n\) then it’ll remain bounded.

Additionally, if \[|c| > \frac{2}{5\left(\frac{5}{7}\right)^3} = \frac{686}{625} = 1.0976\] all the critical points are certainly bounded, because \(|z_0| < \frac{5}{7}\).

Note: this does not imply it converges to \(0\), but the technique of the next section could maybe be adapted. I think boundedness is enough but I’m not 100% sure.

# 3 Escape To Infinity

Assume \(|c| \le \frac{686}{625}\).

Suppose \(|z_n| > (1 + \epsilon) R\) with some \(\epsilon > 0\). If that implies \(|z_{n+1}| > (1 + \epsilon)^2 R\), then \(|z_{n + m}| > (1 + \epsilon)^{m+1} R \to \infty\) as \(m \to \infty\).

Concretely, let \(R = \frac{1}{\sqrt[3]{|c|}}\) and \(\epsilon = \frac{4}{15}\).

Writing \(|c| = \frac{1}{b^k}\) for some \(k\) and \(b > 1\), then \(R = b^{k/3}\). Now

\[\begin{aligned} |z_{n+1}| &= |z_n^2 + c z_n^5| \\ &> \left| |z_n|^2 - |c| |z_n|^4 \right| \\ &> \left| (1 + \epsilon)^2 R^2 - |c| (1 + \epsilon)^5 R^5 \right| \\ &= (1 + \epsilon)^2 \left| b^{2k/3} - (1+\epsilon)^3 \frac{b^{5k/3}}{b^k} \right| \\ &= (1 + \epsilon)^2 ((1 + \epsilon)^3 - 1) b^{2k/3} \\ &= (1 + \epsilon)^2 R \times ((1 + \epsilon)^3 - 1) R \end{aligned}\]

In the second part of the product, substitute \(\epsilon = \frac{4}{15}\), and having assumed \(|c| \le \frac{686}{625}\) we know \(R \ge \sqrt[3]{\frac{625}{686}}\), that is,

\[\begin{aligned} |z_{n+1}| &> (1 + \epsilon)^2 R \times \frac{3484}{3375} \sqrt[3]{\frac{625}{686}} \\ &= (1 + \epsilon)^2 R \times 1.000744019\ldots \\ &> (1 + \epsilon)^2 R \end{aligned}\]

Therefore, if \(|c| \le \frac{686}{625} = 1.0976\) then \[|z_n| > \frac{19}{15 \sqrt[3]{|c|}}\] implies that that the iteration escapes to infinity.

Moreover, if \(0 < |c| < 0.01\), then \(|z_1| > \frac{19}{15 \sqrt[3]{|c|}}\), that is this region of the \(c\) plane always escapes to infinity (for \(z_0\) a non-zero critical point). The bound 0.01 could be increased with more effort.

# 4 Special c

The right-most tip of the escaping region (see visualisation below) is pre-periodic, with positive real \(c\) satisfying \(f_c(f_c(z_0(c))) = f_c(z_0(c))\) for the real critical point and \(f_c(f_c(f_c(z_0(c)))) = f_c(z_0(c))\) for the complex critical points (which means all the critical points are bounded and the filled-in Julia set has a single component).

Using SageMath, the exact value can be found as the cube of a root of a quintic with algebraic coefficients:

f(c, z) = z^2 + c * z^5
for cp in solve(diff(f(c, z), z) == 0, z):
  try:
    g(c) = (f(c, f(c, z)) - f(c, z)).substitute(cp).expand()
    h(x) = (g(x^3) * x^7).canonicalize_radical()
    P = sum([ QQbar(H[0]) * polygen(QQbar)^H[1] for H in h(x).coefficients() ])
    c0 = QQbar.polynomial_root(P, CIF(RIF(0.6, 0.7), RIF(-0.1, 0.1)))^3
    z0 = QQbar(- (2 / (5 * c0))^(1/3))
    z1 = QQbar((- 2 / (5 * c0))^(1/3))
    print(all([f(c0, z0) == f(c0, f(c0, z0)), f(c0, z1) == f(c0, f(c0, f(c0, z1)))]))
    print(h(x))
    print(P)
    print(CIF(c0))
  except:
    pass

(download: z2cz5.sage) which outputs:

True
-3/1953125*5^(2/3)*(15625*5^(2/3)*2^(2/3)*x^5 - 18750*2^(1/3)*x^3 - 648*2^(1/3))
-0.3257301139913888?*x^5 + 0.1061001071608432?*x^3 + 0.003666819703478739?
0.2294487977025897?

that is, the special \(c\) is \(c = 0.229448797702589\ldots\).

I used SageMath version 9.5, Release Date: 2022-01-30 as found in Debian Bookworm (current testing distribution) on 2023-03-09.

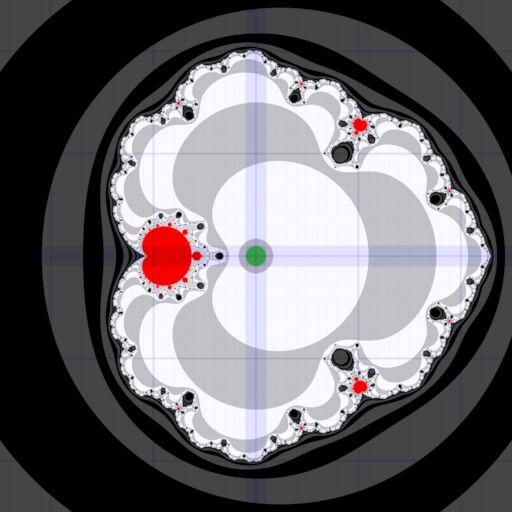
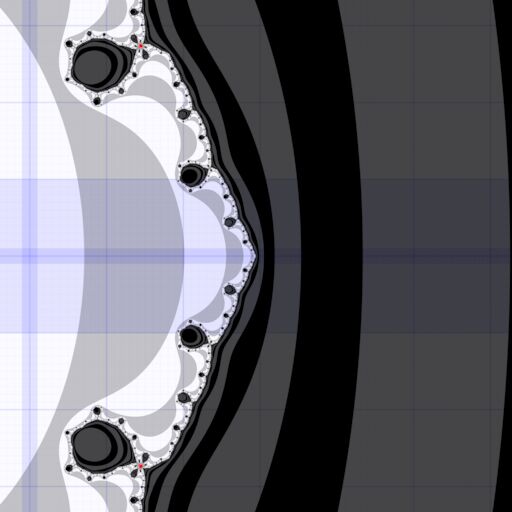
# 5 Visualisation

Source code for Fragmentarium (FragM fork version Fragmentarium 2.5.7.221026 Digilantism with include path Examples/Claude): z2cz5.frag

• green: critical point proven to escape to infinity (center) or remain bounded (outside)
• red: no decision reached after 1000 iterations
• light: critical point escapes to infinity (filled-in Julia set has infinitely-many components)
• dark: critical point remains bounded (filled-in Julia set has a single component)
• blue coordinate grid at 1, 0.1, 0.01, … spacing

Wide view:

Zoomed view:

Close up view of special \(c\):

Animation of filled-in Julia set near special \(c\) for real \(c \pm \frac{1}{10}\):