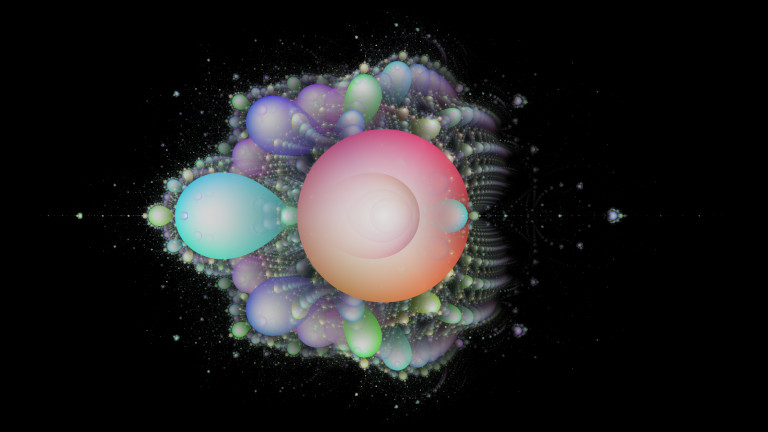
# Buddhabrot

# 1.1 Buddhabrot

The Buddhabrot accumulates each \(z\) in a histogram, for \(z \to z^2 + c\) diverging to infinity. That is, \(c\) is not in the Mandelbrot set.

Often rotated so the axis of mirror symmetry is vertical.

# 1.2 Nebulabrot

The Nebulabrot accumulates each \(z\) in a histogram corresponding to the iteration count at escape from radius \(2\) for \(z \to z^2 + c\) diverging to infinity. That is, \(c\) is not in the Mandelbrot set. Typically there are 3 histogram layers, one each for R G B channels, with different iteration count ranges for each.

# 1.3 Spectral Buddhabrot

“Spectral” techniques with more than 3 layers are possible:

This is my render from 2018.

# 1.4 Anti-Buddhabrot

The Anti-Buddhabrot accumulates each \(z\) in a histogram, for \(z \to z^2 + c\) not diverging to infinity. That is, \(c\) is in the Mandelbrot set.

# 1.5 Ultimate Anti-Buddhabrot

The Ultimate Anti-Buddhabrot accumulates each \(z\) in its period \(p\) limit cycle (found by Newton’s method or similar), weighted by \(\frac{1}{p}\), for \(z \to z^2 + c\) converging to a periodic attractor. That is, \(c\) is in the closure of the hyperbolic components of the Mandelbrot set. See defining blog post Ultimate Anti-Buddhabrot (2013).

# 1.6 Boundary Ultimate Anti-Buddhabrot

The Boundary (Ultimate) Anti-Buddhabrot is the (Ultimate) Anti-Buddhabrot with \(c\) restricted to the boundary of the Mandelbrot set. See related blog post Vector Buddhabrot (2016).

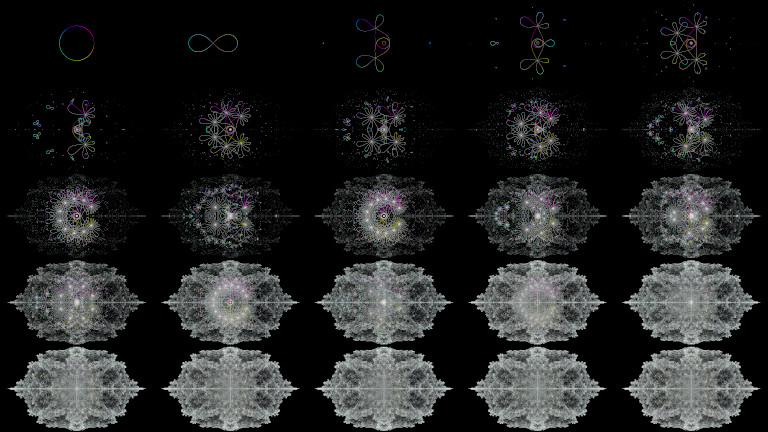
With periods up to 6, to show construction:

With periods up to 27, to show eventual shape:

These are my renders from January 2024.

# 1.7 Buddhagram

The (((Boundary) Ultimate) Anti-)Buddhagram is the corresponding 4D “hologram” structure (2 complex dimensions) of \((z,c)\). See related blog post Ultimate Anti-Buddhagram (2019).

# 2.1 The Buddhabrot Exists

Experimental evidence suggests that the contribution of orbits between iteration count \(2^n\) and iteration count \(2^{n+1}\) seems to reduce as \(n\) increases:

If the contributions reduce fast enough, then the limit should be well-defined.

See also my M.SE question from August 2015, is the Buddhabrot well-defined?.

# 2.2 The Anti-Buddhabrot Exists

The area of the Mandelbrot set is finite, because it is contained within a disc of radius 2. Moreover all the iterates are contained within a disc of radius 2. So if \(n\) iterations are plotted, weighted by \(\frac{1}{n}\), then the total contribution should remain the same.

# 2.3 The Ultimate Anti-Buddhabrot Exists

There are \(p\) points in each limit cycle, so they will be hit \(\frac{n}{p}\) times on average. By the previous argument, the total contribution should be the same when points are weighted by \(\frac{1}{p}\).

# 2.4 The Ultimate Anti-Buddhabrot Is The Limit Of The Anti-Buddhabrot

Skip the first finitely-many \(N\) iterations, which are insignificant as \(n \to \infty\). Then the Ultimate Anti-Buddhabrot is unchanged, while the Anti-Buddhabrot gets closer to the Ultimate Anti-Buddhabrot, as the periodic attractors attract. Then let \(N \to \infty\); does the Anti-Buddhabrot keep getting closer, and fast enough?

Boundary points attract weakly: does this conjecture’s status change when considering the Boundary sets?

# 2.5 The Boundary Ultimate Anti-Buddhabrot Exists

If boxes are weighted by \(c\) area divided by period, the contributions are all zero: the boundaries of hyperbolic components, (are) a set of Hausdorff dimension 1 (comment by Lasse Rempe).

If lines are weighted by \(c\) length divided by period, experimentally (up to periods in the 20s) the contributions seem to increase as the period increases:

However, when normalized by total contributions, the accumulation does seem to converge to a limiting distribution:

To be investigated further…

# 2.6 The Boundary Ultimate Anti-Buddhabrot Is Not The Limit Of The Buddhabrot

The overall contributions to the Buddhabrot reduce when increasing iteration count, because the area gets smaller faster than the iteration count increases. This means that the argument of skipping finitely-many \(N\) iterations does not work, because the initial iterations are significant.

# 3.1 Spectral Buddhabrot

code.mathr.co.uk/fractal-bits/buddhabrot

git clone https://code.mathr.co.uk/fractal-bits.git
cd fractal-bits/buddhabrot

I forgot how this one works.

# 3.2 Ultimate Anti-Buddhabrot

code.mathr.co.uk/fractal-bits/ultimate-anti-buddha

git clone https://code.mathr.co.uk/fractal-bits.git
cd fractal-bits/ultimate-anti-buddha
make anti
mkdir output
cd output
../anti

This one does a non-incremental first stage in several passes, which takes an amount of time dependent on the memory limit set in the code: default 1GB in the repo, I raise it to 24GB on my desktop before compiling, or even 128GB if I have swap space enabled - the lower bound on final memory residency is the limit divided by 5, as soon as this limit is exceeded at the end of a pass the first stage ends. At the end of the first stage a checkpoint is made, which takes as much disk space as memory in use. Resuming from the checkpoint is automatic.

The second stage is incremental, with an unlimited number of passes, each taking approximately twice as long as the previous one. At the end of each pass images are saved.

# 3.3 Boundary Ultimate Anti-Buddhabrot

code.mathr.co.uk/mandelbrot-graphics/c/bin/m-uabb-vector.c

git clone https://code.mathr.co.uk/mandelbrot-graphics.git
# see documentation for other dependencies
cd mandelbrot-graphics/c/bin
make m-uabb-vector
mkdir output
cd output
../m-uabb-vector

This one does incremental rendering until interrupted. Needs NETPBM to save images (PPM is piped to pnmtopng). Resume from last checkpoint with ./m-uabb-vector NN where NN is the latest accum-NN.raw.gz. Each level takes about twice as long as the previous one; levels 1-27 take about 10 hours wall-clock on 16-thread AMD 2700X CPU.

# 4.1 Ghost Ship

Buddhabrot techniques applied to the Burning Ship fractal.

# 4.2 Inverse Iteration

Buddhabrot techniques applied to \(z \to \pm \sqrt{z - c}\) (the inverse iteration method for quadratic Julia sets) give an image somewhat similar to the Boundary Ultimate Anti-Buddhabrot.