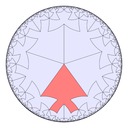
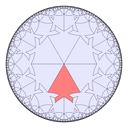
Fish variations

I drew part of a \(\{6,3\}\) tiling of the plane with stylized fish, the full tiling would look more like:

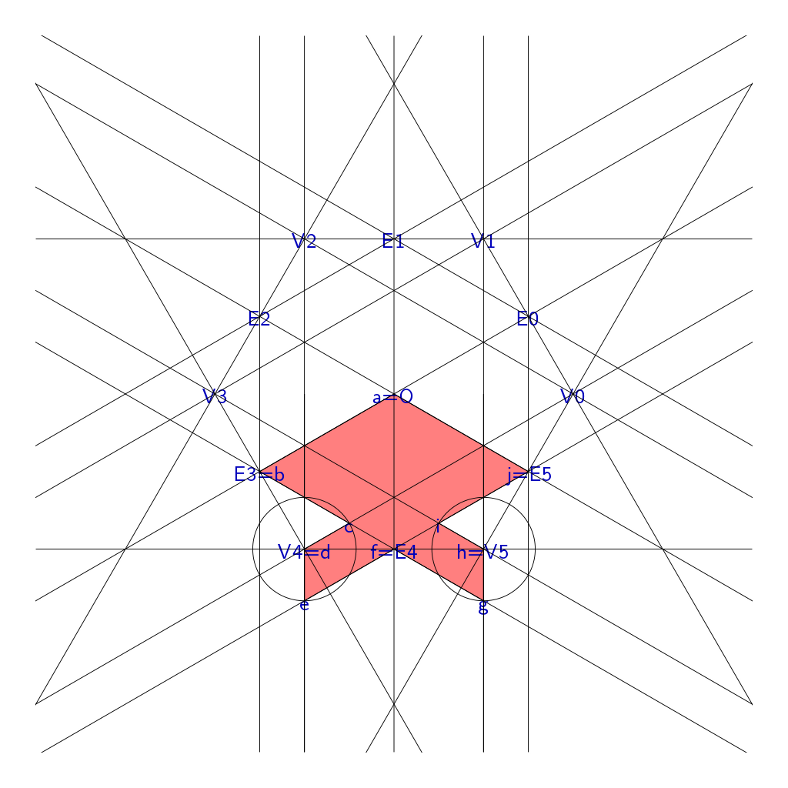
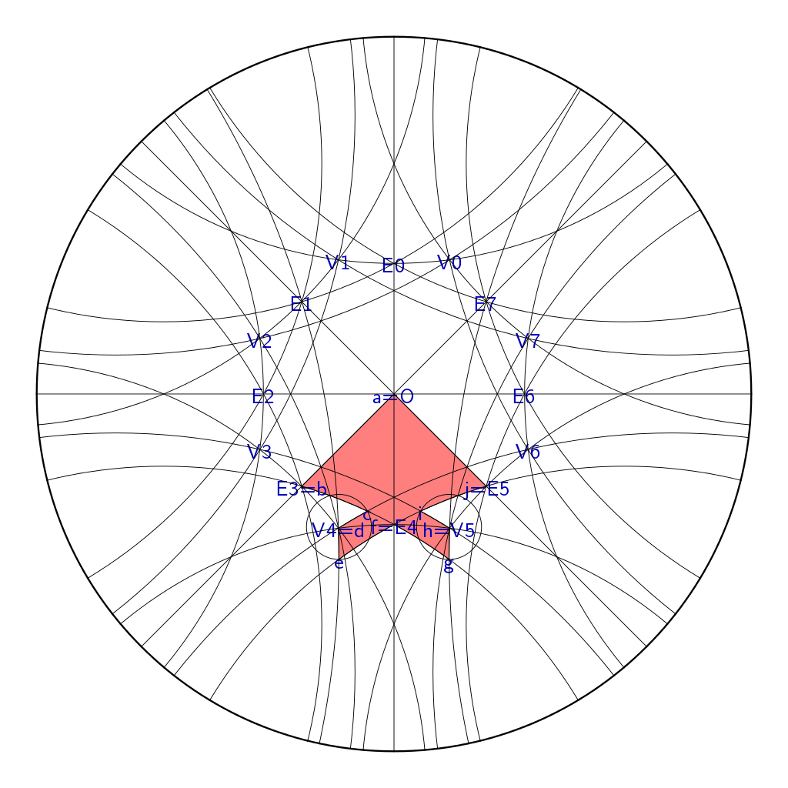
The shape of the fish is constructed with compass and straightedge. First create a hexagon with origin \(O\), vertices \(V_i\) and edge midpoints \(E_i\). Define \(\operatorname{line}(p, q)\) as the line passing through \(p\) and \(q\), and \(\operatorname{circle}(p, q)\) as the circle centered at \(p\) passing through \(q\), the remaining points of the fish can be found:
\[\begin{align*} c &= \operatorname{line}(E_3, E_4) \cap \operatorname{line}(V_4, V_0) \\ i &= \operatorname{line}(E_4, E_5) \cap \operatorname{line}(V_5, V_3) \\ e &= \operatorname{circle}(V_4, c) \cap \operatorname{line}(E_4, E_5) \text{ furthest from } E_4 \\ g &= \operatorname{circle}(V_5, i) \cap \operatorname{line}(E_4, E_3) \text{ furthest from } E_4 \end{align*}\]
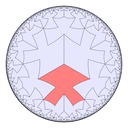
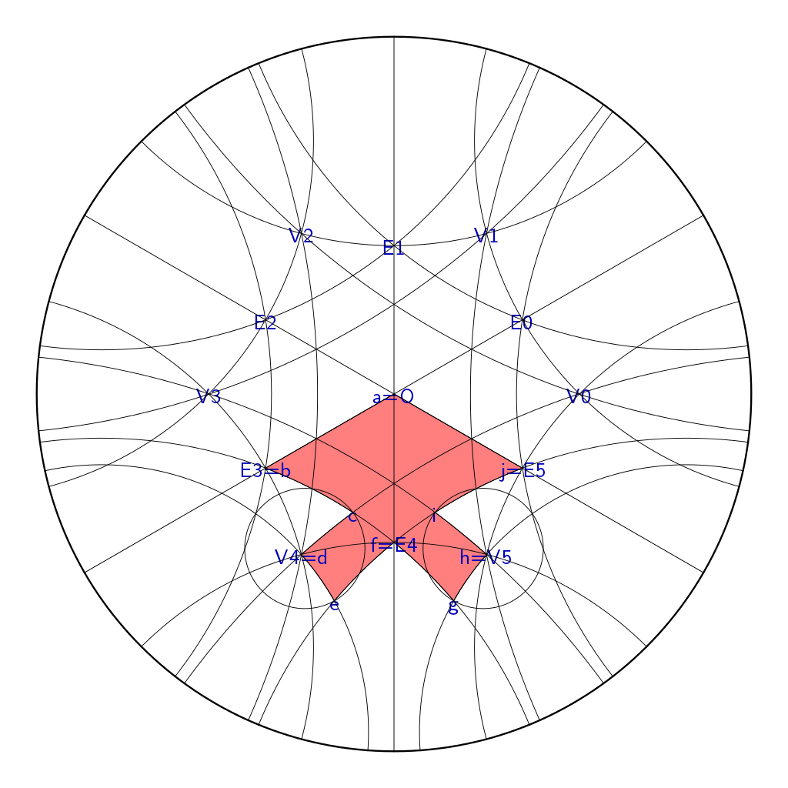
It turns out that this construction is also valid in hyperbolic space, because nothing depends on the existence of unique parallels. Here's a diagram showing four hexagons about each vertex in the Poincaré disk model of hyperbolic geometry:
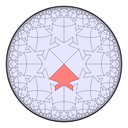
And another showing three octagons about each vertex:
In hyperbolic space areas and angles are connected. The key step in making hyperbolic tilings is finding the side lengths of the fundamental triangle, between the origin \(O\), vertex \(V\), and midpoint of neighbouring edge \(E\). All the angles are known given the Schläfli symbol \(\{p,q\}\): they are \((\pi/p, \pi/q, \pi/2)\). The side lengths can be calculated using the hyperbolic law of cosines:
\[\begin{align*} \cosh(|OV|) = \frac{\cos(\pi/2) + \cos(\pi/p) \cos(\pi/q)}{\sin(\pi/p) \sin(\pi/q)} \\ \cosh(|OE|) = \frac{\cos(\pi/q) + \cos(\pi/p) \cos(\pi/2)}{\sin(\pi/p) \sin(\pi/2)} \\ \cosh(|EV|) = \frac{\cos(\pi/p) + \cos(\pi/q) \cos(\pi/2)}{\sin(\pi/q) \sin(\pi/2)} \end{align*}\]
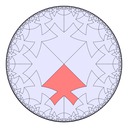
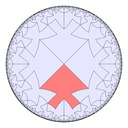
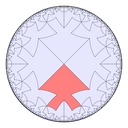
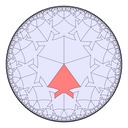
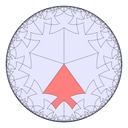
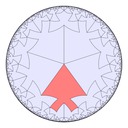
Here are some fish tiling variations in hyperbolic space, with Poincaré half-plane model representations too:
I wrote the implementation in Haskell. My code consists of a library for compass-and-straightedge construction with instances for Euclidean (flat) and hyperbolic (negatively curved) space with spherical (positively curved) space a possibility in the future, along with embeddings into Euclidean space for visualisation using the Diagrams library. The cool part is that the same code generates all the variations from a few parameters.