Mandelbook

Graphical Algorithms

Membership

Membership rendering

Colour according to whether the iterations diverge to infinity or not, within a fixed maximum number of iterations \(N\) and escape radius \(R \ge 2\). The disconnected specks visible in the image turn out to be copies of the whole, and despite appearances the Mandelbrot set is connected.

C99 Code

#include <complex.h>
#include <stdbool.h>

bool m_membership(int N, double R, double _Complex c)
{
    double _Complex z = 0;
    for (int n = 0; n < N; ++n)
    {
        if (cabs(z) > R)
            return false;
        z = z * z + c;
    }
    return true;
}

Escape Time

Escape time rendering

Colour according to the integer number of iterations \(n\) at which \[\left|z_n\right| > R \ge \left|z_{n-1}\right|\] where escape radius \(R \ge 2\).

C99 Code

#include <complex.h>

int m_escape_time
    (int N, double R, double _Complex c)
{
    double _Complex z = 0;
    for (int n = 0; n < N; ++n)
    {
        if (cabs(z) > R)
            return n;
        z = z * z + c;
    }
    return -1;
}

Binary Decomposition

Binary decomposition rendering

Colour according to the sign of \(\Im z\) (the first escaped iterate). Increasing escape radius is necessary to align edges between layers. Escape radius around \(R = 25\) makes the decomposed cells roughly square.

C99 Code

#include <complex.h>
#include <stdbool.h>

bool m_binary_decomposition
    (int N, double R, double _Complex c)
{
    double _Complex z = 0;
    for (int n = 0; n < N; ++n)
    {
        if (cabs(z) > R)
            return cimag(z) > 0;
        z = z * z + c;
    }
    return true;
}

Continuous Dwell

Continuous dwell rendering

Vepstas (1997) derives the renormalized continuous escape time:

\[\mu = n + 1 - \log_2 \left( \log \left|z\right| \right)\]

In the above formula, the value of \(\mu\) is almost completely independent of the iteration count, and of the escape radius, despite the fact that the right-hand-side of the equation is explicitly dependent on both of these quantities. The renormalized iteration count \(\mu\) depends only on \(c\), and is a piecewise-continuous, differentiable function thereof. By using a different analysis, it can be seen that the renormalized iteration count \(\mu\) is in fact the residue remaining when a pole (due to the infinite sum) is removed. That is, the value of \(\mu\) closely approximates the result of having iterated to infinity, that is, of having an infinite escape radius, and an infinite maximum iteration count.

C99 Code

#include <complex.h>
#include <math.h>

double m_continuous_dwell
    (int N, double R, double _Complex c)
{
    double _Complex z = 0;
    for (int n = 0; n < N; ++n)
    {
        if (cabs(z) > R)
            return n + 1 - log2(log(cabs(z)));
        z = z * z + c;
    }
    return -1;
}

Exterior Coordinates

Exterior coordinates rendering

Escape radius around \(R = 25^2\) makes the exterior grid cells roughly square. The imaginary part of \(e\) is linearized to avoid shape distortion. \[ \Re e = \frac{\arg z}{2 \pi} \mod 1 \] \[ \Im e = 2 - \frac{\log \left|z\right|}{\log R} \]

The exterior coordinate \(e\) can be used to look up pixel colours from an image texture, but care must be taken to avoid glitches at the cell boundaries if automatic derivatives are used for mipmapped anti-aliasing. The calculation of the derivatives must be modified to account for the wrapped space.

Heiland-Allen (2012a) has an example of animating image texture during a zoom video.

C99 Code

#include <complex.h>
#include <math.h>

const double pi = 3.141592653589793;

double _Complex m_exterior_coordinates
    (int N, double R, double _Complex c)
{
    double _Complex z = 0;
    for (int n = 0; n < N; ++n)
    {
        if (cabs(z) > R)
            return fmod(1 + carg(z) / (2 * pi), 1)
                + I * (2 - log(cabs(z)) / log(R));
        z = z * z + c;
    }
    return 0;
}

Dwell Gradient

Dwell gradient rendering

\[\begin{aligned} v &= \left(\begin{matrix}\mu - \mu_x \\ \mu - \mu_y \\ s\end{matrix}\right) \\ g &= \frac{v_3}{\left|v\right|} \end{aligned}\]

where \(\mu_x\) and \(\mu_y\) are the continuous dwells of neighbouring pixels to the above and left of the pixel under consideration, and \(s > 0\) is a parameter that controls the strength of the effect. \(0 \le g \le 1\) colours the boundary of the set where iteration count goes up increasingly quickly. Define \(\mu\) to be large and negative for pixels that didn't escape.

Heiland-Allen (2014f) also describes using \(\tan^{-1} \frac{v_2}{v_1}\) as hue for a rainbow colouring of dwell slope.

C99 Code

#include <complex.h>
#include <math.h>

const double pi = 3.141592653589793;

double _Complex m_dwell_gradient
    (int N, double R, double s, double d, double _Complex c)
{
    double m  = m_continuous_dwell(N, R, c);
    double mx = m_continuous_dwell(N, R, c + d);
    double my = m_continuous_dwell(N, R, c + d * I);
    double vx = m - mx;
    double vy = m - my;
    double vz = s;
    double vm = sqrt(vx * vx + vy * vy + vz * vz);
    return vz / vm;
}

Exterior Distance

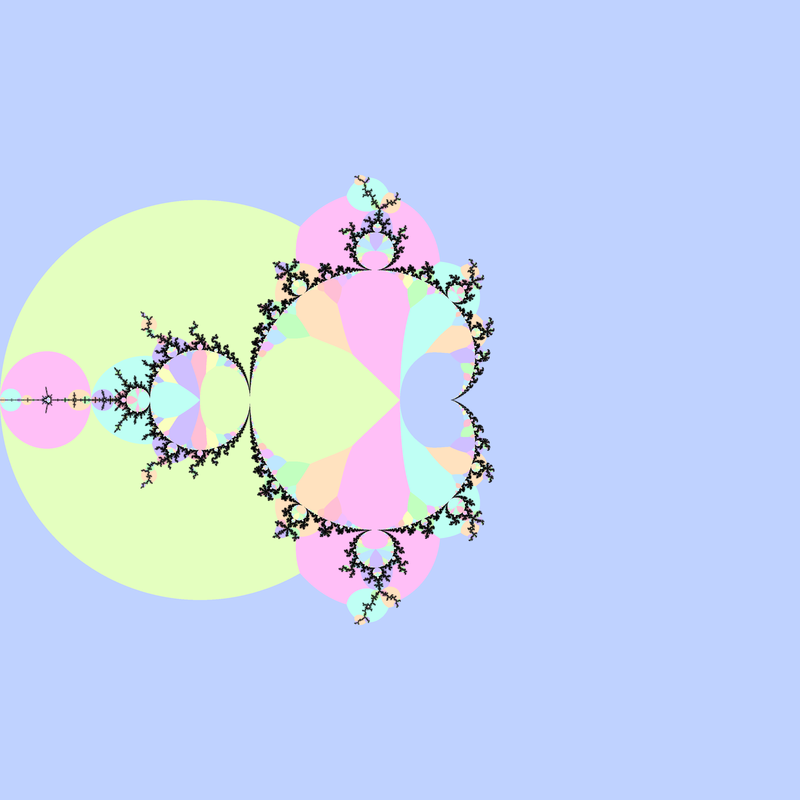
Exterior distance rendering

Formalizes the dwell gradient idea, in that closeness of dwell bands is related to closeness to the boundary of the set. In Peitgen and Saupe (1988 Appendix D), Yuval Fisher bounds the distance \(d(c, M)\) between a point \(c\) outside \(M\) and \(M\) itself by:

\[\frac{\sinh G(c)}{2 e^{G(c)} \left|\frac{d}{dc}G(c)\right|} < d(c, M) < \frac{2 \sinh G(c)}{\left|\frac{d}{dc}G(c)\right|}\]

where \(G(c)\) is the potential of the point \(c\). The upper bound can be approximated by using a large escape radius; for escaped \(z\):

\[d = 2 \frac{\left|z\right| \log \left|z\right|} {\left|\frac{\partial}{\partial c}z\right|}\]

There is a point in the Mandelbrot set within \(d\). No point in the Mandelbrot set is within \(\frac{d}{4}\). Compare with pixel spacing to know if the Mandelbrot set might intersect a pixel.

A complex-valued distance estimate (with directional information) can be calculated by:

\[d = 2 \frac{z \log \left|z\right|}{\frac{\partial}{\partial c}z}\]

Heiland-Allen (2010b) and Heiland-Allen (2010c) use distance estimates to give progressively finer approximations to the exterior, while Heiland-Allen (2014e) describes an adaptive supersampling method.

C99 Code

#include <complex.h>
#include <math.h>

const double pi = 3.141592653589793;

double _Complex m_exterior_distance
    (int N, double R, double _Complex c)
{
    double _Complex z = 0;
    double _Complex dc = 0;
    for (int n = 0; n < N; ++n)
    {
        if (cabs(z) > R)
            return 2 * z * log(cabs(z)) / dc;
        dc = 2 * z * dc + 1;
        z = z * z + c;
    }
    return 0;
}

Atom Domains

Atom domains rendering

Munafo (1996) and Peitgen and Richter (1986, fig. 34 on page 61) describe atom domains in the Mandelbrot set, defined as the index \(p \ge 1\) at which \(\left|z_p\right|\) is minimized during iteration of \(z_0 = 0\) and \(z_{n+1} = z_n^2 + c\). Atom domains surround hyperbolic components of the same period, and are generally much larger than the components themselves, which makes them useful for finding components.

Heiland-Allen (2012c) describes a modification of atom domains, which makes smaller domains more visible.

C99 Code

#include <complex.h>
#include <math.h>

int m_atom_domains(int N, double R, double _Complex c)
{
    double _Complex z = c;
    double mp = 1.0 / 0.0;
    int p = 0;
    for (int n = 1; n < N; ++n)
    {
        double zp = cabs(z);
        if (zp < mp)
        {
            mp = zp;
            p = n;
        }
        z = z * z + c;
    }
    return p;
}

Misiurewicz Domains

Misiurewicz domains rendering

Preperiodic points in the Mandelbrot set are called Misiurewicz points, and they have repelling orbits (periodic hyperbolic components have attracting orbits). Atom domains show the period with the preperiod fixed at \(0\), while for Misiurewicz domains show the preperiod with the period fixed.

Heiland-Allen (2015c) defines the Misiurewicz domain for period \(p \ge 1\) as the index \(q\) at which \(\left|z_{p + q} - z_q\right|\) is minimized. Misiurewicz domains surround Misiurewicz points whose period divides \(p\), and are much larger than a single point, which makes makes them useful for finding Misiurewicz points.

C99 Code

#include <complex.h>

int m_misiurewicz_domains
    (int N, int p, double _Complex c)
{
    int q = 0;
    double _Complex z = c;
    double _Complex zp = c;
    double mq = 1.0 / 0.0;
    for (int n = 0; n < p; ++n)
        z = z * z + c;
    for (int n = 0; n < N - p; ++n)
    {
        double zq = cabs(z - zp);
        if (zq < mq)
        {
            mq = zq;
            q = n;
        }
        z = z * z + c;
        zp = zp * zp + c;
    }
    return q;
}

Interior Coordinates

Interior coordinates rendering

Heiland-Allen (2013c) derives an algorithm for calculating interior coordinates \(b\), and it turned out that only periods that are "partials" (corresponding to atom domains) need be considered:

• For each period p, starting from 1 and increasing:
• If \(|F^p(0, c)|\) reaches a new minimum:
  • Find \(z_0\) such that \(F^p(z_0,c)=z_0\) using Newton's method in one complex variable ("attractor", with initial guess \(F^p(0,c)\));
  • Find \(b =\frac{\partial}{\partial z} F^p(z_0,c)\);
  • If \(|b| \le 1\) then return \(b\), otherwise continue with the next \(p\).

C99 Code

#include <complex.h>

double _Complex m_interior_coordinates
    (int N, int M, double _Complex c)
{
    double _Complex z = 0;
    double mz = 1.0 / 0.0;
    for (int n = 0; n < N; ++n)
    {
        z = z * z + c;
        double zp = cabs(z);
        if (zp < mz)
        {
            mz = zp;
            double _Complex w = m_attractor(z, n, c, M);
            double _Complex dw = 1;
            for (int m = 0; m < n; ++m)
            {
                dw = 2 * w * dw;
                w = w * w + c;
            }
            if (cabs(dw) <= 1)
                return dw;
        }
    }
    return 0;
}

Interior Distance

Interior distance rendering

The formula for interior distance estimation is:

\[d = \frac{1-\left|\frac{\partial}{\partial{z}}\right|^2} {\left|\frac{\partial}{\partial{c}}\frac{\partial}{\partial{z}} + \frac{\left(\frac{\partial}{\partial{z}}\frac{\partial}{\partial{z}}\right) \left(\frac{\partial}{\partial{c}}\right)} {1-\frac{\partial}{\partial{z}}}\right|}\]

where the derivatives are evaluated at \(z_0\) satisfying \(F^p(z_0, c) = z_0\).

Following Heiland-Allen (2014c), simple code for distance estimate rendering now looks something as follows; more involved algorithms that provide a significant speed-up can be found at the reference.

C99 Code

#include <complex.h>
#include <math.h>

double cnorm(double _Complex z)
{
  return creal(z) * creal(z) + cimag(z) * cimag(z);
}

double m_interior_distance
    (double _Complex z0, double _Complex c, int p)
{
    double _Complex z = z0;
    double _Complex dz = 1;
    double _Complex dzdz = 0;
    double _Complex dc = 0;
    double _Complex dcdz = 0;
    for (int m = 0; m < p; ++m)
    {
        dcdz = 2 * (z * dcdz + dz * dc);
        dc = 2 * z * dc + 1;
        dzdz = 2 * (dz * dz + z * dzdz);
        dz = 2 * z * dz;
        z = z * z + c;
    }
    return (1 - cnorm(dz))
        / cabs(dcdz + dzdz * dc / (1 - dz));
}

double m_distance(int N, double R, double _Complex c)
{
    double _Complex dc = 0;
    double _Complex z = 0;
    double m = 1.0 / 0.0;
    int p = 0;
    for (int n = 1; n <= N; ++n)
    {
        dc = 2 * z * dc + 1;
        z = z * z + c;
        if (cabs(z) > R)
            return 2 * cabs(z) * log(cabs(z)) / cabs(dc);
        if (cabs(z) < m)
        {
            m = cabs(z);
            p = n;
            double _Complex z0 = m_attractor(z, c, p);
            double _Complex w = z0;
            double _Complex dw = 1;
            for (int k = 0; k < p; ++k)
            {
                dw = 2 * w * dw;
                w = w * w + c;
            }
            if (cabs(dw) <= 1)
                return m_interior_distance(z0, c, p);
        }
    }
    return 0;
}

Numerical Algorithms

Nucleus

The nucleus \(c\) of a hyperbolic component of period \(p\) satisfies:

\[F^p(0,c) = 0\]

Applying Newton's method in one complex variable:

\[c_{m+1} = c_m - \frac{F^p(0, c_m)}{\frac{\partial}{\partial c}F^p(0, c_m)}\]

A reasonable starting guess for Newton's method is within the atom domain of the component (Heiland-Allen (2012b)).

C99 Code

#include <complex.h>

double _Complex m_nucleus
    (double _Complex c0, int p, int n)
{
    double _Complex c = c0;
    for (int m = 0; m < n, ++m)
    {
        double _Complex z = 0;
        double _Complex dc = 0;
        for (int i = 0; i < period; ++i)
        {
            dc = 2 * z * dc + 1;
            z = z * z + c;
        }
        c = c - z / dc;
    }
    return c;
}

Examples

\(c_0 = -1.8\), \(p = 3\): \[\begin{aligned} c_0 &= -1.8 \\ c_1 &= -1.75(78298397040690\ldots) \\ c_2 &= -1.7548(913878280483\ldots) \\ c_3 &= -1.754877666(5449095\ldots) \\ c_4 &= -1.7548776662466929(\ldots) \end{aligned}\]

\(c_0 = i\), \(p = 4\): \[\begin{aligned} c_0 &= & i \\ c_1 &= -0.(11926605504587157\ldots) &+ 0.(9357798165137615\ldots) i \\ c_2 &= -0.(23004008246918839\ldots) &+ 1.0(769584254327267\ldots) i \\ c_3 &= -0.1(8143326956347502\ldots) &+ 1.0(265172581955131\ldots) i \\ c_4 &= -0.15(552525333120717\ldots) &+ 1.0(295018249244792\ldots) i \\ c_5 &= -0.1565(4521565515017\ldots) &+ 1.0322(758207945100\ldots) i \\ c_6 &= -0.1565201(7318905109\ldots) &+ 1.03224710(96777757\ldots) i \\ c_7 &= -0.1565201668337550(8\ldots) &+ 1.032247108922831(6\ldots) i \\ c_8 &= -0.1565201668337550(5\ldots) &+ 1.0322471089228318(\ldots) i \\ c_9 &= -0.1565201668337550(3\ldots) &+ 1.0322471089228318(\ldots) i \\ c_{10} &= -0.15652016683375508(\ldots) &+ 1.0322471089228318(\ldots) i \end{aligned}\]

Attractor

The attractor \(w\) of a point \(c\) within a hyperbolic component of period \(p\) consists of \(p\) points, each satisfying:

\[F^p(w,c) = w\]

Applying Newton's method in one complex variable:

\[ w_{m+1} = w_m - \frac{F^p(w_m, c) - w_m} {\frac{\partial}{\partial z}F^p(w_m, c) - 1}\]

A reasonable starting guess for Newton's method is \(w_0 = F^p(0, c)\).

C99 Code

#include <complex.h>

double _Complex m_attractor
    (double _Complex w0, double _Complex c, int p, int n)
{
    double _Complex w = w0;
    for (int m = 0; m < n; ++m)
    {
        double _Complex z = w;
        double _Complex dz = 1;
        for (int i = 0; i < p; ++i)
        {
            dz = 2 * z * dz;
            z = z * z + c;
        }
        w = w - (z - w) / (dz - 1);
    }
    return w;
}

Examples

\(c = 0.5 i\), \(p = 1\): \[\begin{aligned} w_0 &= & 0.5 i \\ w_1 &= -0.1(2500000000000000\ldots) &+ 0.3(7500000000000000\ldots) i \\ w_2 &= -0.1360(2941176470587\ldots) &+ 0.393(38235294117646\ldots) i \\ w_3 &= -0.136009(77572623132\ldots) &+ 0.393075(72864807383\ldots) i \\ w_4 &= -0.13600982475703(358\ldots) &+ 0.3930756888787(0914\ldots) i \\ w_5 &= -0.13600982475703449(\ldots) &+ 0.39307568887871164(\ldots) i \end{aligned}\]

\(c = -1.1 + 0.1 i\), \(p = 2\): \[\begin{aligned} w_0 &= 0.1 &- 0.12 i \\ w_1 &= 0.09(5782435714904968\ldots) &- 0.08(4585559740811250\ldots) i \\ w_2 &= 0.09749(9098252211647\ldots) &- 0.0836(77122424611575\ldots) i \\ w_3 &= 0.097497068(763801931\ldots) &- 0.0836824188(71189990\ldots) i \\ w_4 &= 0.097497068806210202(\ldots) &- 0.083682418894370822(\ldots) i \end{aligned}\]

Interior Point

The interior point \(b\) at internal angle \(\theta\) measured in turns and internal radius \(r \in [0,1]\) within a hyperbolic component of period \(p\) satisfies:

\[\begin{aligned} F^p(w,b) &= w \\ \frac{\partial}{\partial z}F^p(w,b) &= r e^{2 \pi i \theta} = t \end{aligned}\]

Applying Newton's method in two complex variables:

\[\begin{split} \left(\begin{matrix} \frac{\partial}{\partial z}F^p(w_m,b_m) - 1 & \frac{\partial}{\partial c}F^p(w_m,b_m) \\ \frac{\partial}{\partial z}\frac{\partial}{\partial z}F^p(w_m,b_m) & \frac{\partial}{\partial c}\frac{\partial}{\partial z}F^p(w_m,b_m) \end{matrix}\right)\left(\begin{matrix} w_{m+1} - w_m \\ b_{m+1} - b_m\end{matrix}\right) \\ = -\left(\begin{matrix} F^p(w_m,b_m) - w_m \\ \frac{\partial}{\partial z}F^p(w_m,b_m) - t \end{matrix}\right) \end{split}\]

C99 Code

#include <complex.h>

void m_interior_point
( double _Complex *z_out, double _Complex *c_out
, double _Complex z0, double _Complex c0
, double _Complex t, int p, int n
)
{
    double _Complex cc = c0;
    double _Complex zz = z0;
    for (int m = 0; m < n; ++m)
    {
        double _Complex c = cc;
        double _Complex z = zz;
        double _Complex dz = 1;
        double _Complex dc = 0;
        double _Complex dzdz = 0;
        double _Complex dcdz = 0;
        for (int i = 0; i < p; ++i)
        {
            dcdz = 2 * (z * dcdz + dc * dz);
            dzdz = 2 * (z * dzdz + dz * dz);
            dc = 2 * z * dc + 1;
            dz = 2 * z * dz;
            z = z * z + c;
        }
        double _Complex det =
            (dz - 1) * dcdz - dc * dzdz;
        cc = cc - ((dz - 1) * (dz - t)
            - dzdz * (z - zz)) / det;
        zz = zz - (dcdz * (z - zz)
            - dc * (dz - t)) / det;
    }
    *z_out = zz;
    *c_out = cc;
}

Examples

\(r = 1\), \(\theta = \frac{1}{3}\), \(p = 1\) \[\begin{aligned} w_0 &= 0 \\ b_0 &= 0 \\ w_1 &= -0.24999999999999989 + 0.43301270189221935 i \\ b_1 &= -0.24999999999999989 + 0.43301270189221935 i \\ w_2 &= -0.24999999999999989 + 0.43301270189221935 i \\ b_2 &= -0.12499999999999978 + 0.64951905283832900 i \end{aligned}\]

Misiurewicz Point ("Naive")

Heiland-Allen (2013a)

A preperiodic Misiurewicz point \(c\) of preperiod \(q\) and period \(p\) satisfies:

\[ F^{q+p}(0, c) = F^{q}(0, c) \]

A naive implementation of Newton's root finding method iterations for a Misiurewicz point takes the form:

\[ c_{m+1} = c_m - \frac{F^{q+p}(0, c_{m}) - F^{q}(0, c_{m})}{\frac{\partial}{\partial c}F^{q+p}(0, c_m) - \frac{\partial}{\partial c}F^{q}(0, c_m)} \]

C99 Code

#include <complex.h>

double _Complex m_misiurewicz_naive
    (double _Complex c0, int q, int p, int n)
{
    double _Complex c = c0;
    for (int m = 0; m < n; ++m)
    {
        double _Complex z = 0;
        double _Complex dc = 0;
        double _Complex zp = 0;
        double _Complex dcp = 0;
        for (int i = 0; i < q + p; ++i)
        {
            if (i == q)
            {
                zp = z;
                dcp = dc;
            }
            dc = 2 * z * dc + 1;
            z = z * z + c;
        }
        c = c - (z - zp) / (dc - dcp);
    }
    return c;
}

Misiurewicz Point ("Full")

Heiland-Allen (2015b)

A preperiodic Misiurewicz point \(c\) of preperiod \(q\) and period \(p\) satisfies:

\[ F^{q+p}(0, c) = F^{q}(0, c) \] \[ F^{q'+p}(0, c) \neq F^{q'}(0, c) \quad q' < q \]

Dividing by the non-zero factors suggested by the second equation gives:

\[ G(c) = \frac{ F^{q + p}(0, c) - F^{q}(0, c) }{ \prod_{q'=0}^{q-1}\left( F^{q' + p}(0, c) - F^{q'}(0, c) \right) } \]

Applying Newton's root finding method iterations to \(G(c) = 0\) finds the preperiodic Misiurewicz point, with a larger basin of attraction than the "naive" method. However it may not converge as precisely, one approach is to first use this "full" method and then use the "naive" method on its output.

C99 Code

#include <complex.h>

double _Complex m_misiurewicz_full
    (double _Complex c0, int q, int p, int n)
{
    double _Complex c = c0;
    for (int m = 0; m < n; ++m)
    {
        double _Complex z = 0;
        double _Complex dc = 0;
        double _Complex zp = 0;
        double _Complex dcp = 0;
        double _Complex h = 1;
        double _Complex dh = 0;
        for (int i = 0; i < p; ++i)
        {
            dc = 2 * z * dc + 1;
            z = z * z + c;
        }
        for (int i = 0; i < q; ++i)
        {
            double _Complex k = z - zp;
            h = h * k;
            dh = dh + (dc - dcp) / k;
            dc = 2 * z * dc + 1;
            z = z * z + c;
            dcp = 2 * zp * dcp + 1;
            zp = zp * zp + c;
        }
        dh = dh * h;
        double _Complex g = z - zp;
        double _Complex dg = dc - dcp;
        double _Complex f = g / h;
        double _Complex df = (dg * h - g * dh) / (h * h);
        c = c - f / df;
    }
    return c;
}

Child Sizes

Child of a cardioid of size \(s\) at internal angle \(\frac{p}{q}\) has size approximately: \[s' = \frac{s}{q^2} \sin\left(\pi \frac{p}{q}\right)\]

Child of a circle of size \(s\) at internal angle \(\frac{p}{q}\) has size approximately: \[s' = \frac{s}{q^2}\]

Size Estimate

MSet e-notes (2013) presents a method to estimate the size of a hyperbolic component:

Under iterations the critical orbit of period \(p\) consecutively cycles through \(p\) narrow intervals \(S_1 \to S_2 \to \ldots \to S_1\) each of width \(s_j\) (we choose \(S_1\) to include the critical point \(z = 0\)). We expand \(F^p(z, c)\) for small \(z\) (in the narrow central interval \(S_1\)) and \(c\) near its value \(c_0\) at superstability of period-\(p\) attracting orbit. We see that the \(s_j\) are small and the map in the intervals \(S_2, S_3, \ldots S_n\) may be regarded as approximately linear; the full quadratic map must be retained for the central interval. One thus obtains \[z_{n+p} \approx L_p (z_n^2 + b (c - c_0))\] where \(L_p = l_2 l_3 \ldots l_p\) is the product of the map slopes, \(l_n = 2 z_n\) in \(p-1\) noncentral intervals and \(b = 1 + l_2^{-1} + (l_2 l_3)^{-1} + ... + L_n^{-1}\). We take \(L_n\) at \(c = c_0\) and treat it as a constant in narrow window. Introducing \(Z = L_n z\) and \(C = b L_n^2 (c - c_0)\) we get quadratic map \(Z_{n+p} = Z_n^2 + C\). Therefore the window width scales like \((b L_n^2)^{-1}\).

C99 Code

#include <complex.h>

double _Complex m_size_estimate
    (double _Complex c, int p)
{
    double _Complex b = 1;
    double _Complex l = 1;
    double _Complex z = 0;
    for (int i = 1; i < p; ++i)
    {
        z = z * z + c;
        l = 2 * z * l;
        b = b + 1 / l;
    }
    return 1 / (b * l * l);
}

Examples

Cardioid \(c = 0\), \(p = 1\): \[|s| = 1\]

Circle \(c = -1\), \(p = 2\): \[|s| = \frac{1}{2}\]

Cardioid \(c = -1.7548776662466927\), \(p = 3\): \[|s| = 0.019035515913132451\]

Cardioid \(c = -0.15652016683375508 + 1.0322471089228318 i\), \(p = 4\): \[\begin{aligned} |s| &= 0.0084828587005172946 \\ \arg s &= -0.61719885061563229 \end{aligned}\]

Shape Estimate

Dolotin and Morozov (2008 eq. 5.8) derive a shape estimate \(s\), with derivatives evaluated at \(F^p(0,c)\) where \(c\) is a nucleus of period \(p\):

\[s = - \frac{1}{\left(\frac{\partial}{\partial c}\right) \left(\frac{\partial}{\partial z}\right)} \left(\frac{\frac{\partial}{\partial c}\frac{\partial}{\partial c}} {2 \frac{\partial}{\partial c}} + \frac{\frac{\partial}{\partial c}\frac{\partial}{\partial z}} { \frac{\partial}{\partial z}}\right) \]

\(s \approx 0\) corresponds to cardioid-like shapes. \(s \approx 1\) corresponds to circle-like shapes.

C99 Code

#include <complex.h>
#include <stdbool.h>

double _Complex m_shape_estimate
    (double _Complex c, int p)
{
    double _Complex z = c;
    double _Complex dc = 1;
    double _Complex dz = 1;
    double _Complex dcdc = 0;
    double _Complex dcdz = 0;
    for (int i = 1; i < p; ++i)
    {
        dcdc = 2 * (z * dcdc + dc * dc);
        dcdz = 2 * (z * dcdz + dc * dz);
        dc = 2 * z * dc + 1;
        dz = 2 * z * dz;
        z = z * z + c;
    }
    return -(dcdc / (2 * dc) + dcdz / dz) / (dc * dz);
}

bool m_shape_is_cardioid(double _Complex s)
{
    bool d = cabs(s) < cabs(s - 1);
    return d;
}

Examples

\(c = -0.12256116687665361 + 0.74486176661974424 i\), \(p = 3\): \[s = 1.0212516030641008 + 0.047630153362811116 i \approx 1\]

\(c = -0.15652016683375508 + 1.0322471089228318 i\), \(p = 4\): \[s = 0.058425597199448037 + 0.084498085298473649 i \approx 0\]

Domain Size

Heiland-Allen (2013f) derives the atom domain size estimate for a nucleus \(c\) of period \(p\) as:

\[r = \left|\frac{F^q(0, c)}{\frac{\partial}{\partial c} F^p(0, c)}\right|\]

where \(1 \le q < p\) minimizes \(\left|F^q(0, c)\right|\). The atom domain size is approximately 4 times the radius of circle-like components, and typically a lot larger for cardioid-like components.

C99 Code

#include <complex.h>

double m_domain_size(double _Complex c, int p)
{
    double _Complex z = c;
    double _Complex dc = 1;
    double abszq = cabs(z);
    for (int_t q = 2; q <= p; ++q)
    {
        dc = 2 * z * dc + 1;
        z = z * z + c;
        double absz = cabs(z);
        if (absz < abszq && q < p)
            abszq = absz;
    }
    return abszq / cabs(dc);
}

Examples

Circle \(c = -1\), \(p = 2\):

\[r = 1\]

Cardioid \(c = -1.7548776662466929\), \(p = 3\):

\[r = 0.23448676598793725\]

External Ray In

Kawahira (2009) describes an algorithm to trace external rays.

The next point \(r\) along an external ray with current doubled angle \(\theta\) measured in turns, current depth \(p\) and current radius \(R\) satisfies:

\[F^p(0,r)=\lambda R e^{2 \pi i \theta}\]

where \(\lambda < 1\) controls the sharpness of the ray. Applying Newton's method in one complex variable:

\[r_{m+1} = r_m - \frac{F^p(0,r_m) - \lambda R e^{2 \pi i \theta}} {\frac{\partial}{\partial c}F^p(0,r_m)}\]

When crossing dwell bands, double \(\theta\) and increment \(p\), resetting the radius \(R\). Stop tracing when close to the target (for example when within the basin of attraction for Newton's method for nucleus).

C99 Code

#include <complex.h>
#include <math.h>
#include <gmp.h>

struct m_exray_in {
    mpq_t angle;
    mpq_t one;
    int sharpness;
    double er;
    double _Complex c;
    int j;
    int k;
};

struct m_exray_in *m_exray_in_new
    (const mpq_t angle, int sharpness)
{
    m_d_exray_in *ray = malloc(sizeof(*ray));
    mpq_init(ray->angle);
    mpq_set(ray->angle, angle);
    mpq_init(ray->one);
    mpq_set_ui(ray->one, 1, 1);
    ray->sharpness = sharpness;
    ray->er = 65536.0;
    double a = twopi * mpq_get_d(ray->angle);
    ray->c = ray->er * cexp(I * a);
    ray->k = 0;
    ray->j = 0;
    return ray;
}

void m_exray_in_delete(struct m_exray_in *ray)
{
    mpq_clear(ray->angle);
    mpq_clear(ray->one);
    free(ray);
}

double _Complex m_exray_in_step
    (struct m_exray_in *ray, int n)
{
    if (ray->j >= ray->sharpness)
    {
        mpq_mul_2exp(ray->angle, ray->angle, 1);
        if (mpq_cmp_ui(ray->angle, 1, 1) >= 0)
            mpq_sub(ray->angle, ray->angle, ray->one);
        ray->k = ray->k + 1;
        ray->j = 0;
    }
    double r = pow(ray->er,
        pow(0.5, (ray->j + 0.5) / ray->sharpness));
    double a = twopi * mpq_get_d(ray->angle);
    double _Complex target = r * cexp(I * a);
    double _Complex c = ray->c;
    for (int m = 0; m < n; ++m)
    {
        double _Complex z = 0;
        double _Complex dc = 0;
        for (int p = 0; p <= ray->k; ++p)
        {
            dc = 2 * z * dc + 1;
            z = z * z + c;
        }
        c = c - (z - target) / dc;
    }
    ray->j = ray->j + 1;
    ray->c = c;
    return c;
}

External Ray Out

External Angles

Heiland-Allen (2014h)

Symbolic Algorithms

Tuning

Given a periodic external angle pair \((.\overline{a}, .\overline{b})\), tuning of an external angle \(.c\) proceeds by replacing every \(0\) in \(c\) by \(a\) and every \(1\) by \(b\). Here \(a\), \(b\), \(c\) are blocks of binary digits (with \(c\) possibly aperiodic and infinite in extent).

Haskell Code

type ExternalAngle = ([Bool], [Bool])

tuning
  :: (ExternalAngle, ExternalAngle)
  -> ExternalAngle
  -> ExternalAngle
tuning (([], per0), ([], per1)) (pre, per)
  = (concatMap t pre, concatMap t per)
  where
    t False = per0
    t True  = per1

Examples

The external angle pair of the period \(3\) island is: \[\left(.\overline{011}, .\overline{100}\right)\]

The lower angle of the period \(2\) bulb is \(.\overline{01}\), tuned by the period \(3\) island becomes \(.\overline{011100}\) which is the lower angle of the period \(6\) bulb attached to the period \(3\) cardioid at internal angle \(\frac{1}{2}\).

The external angle of the tip of the antenna is \(.1 = .0\overline{1} = .1\overline{0}\), tuned by the period \(3\) island becomes respectively \(.011\overline{100}\) and \(.100\overline{011}\), which are the external angles of the tip of the antenna of the period \(3\) island.

Primary Bulb

The child bulb of the period \(1\) cardioid at internal angle \(\frac{p}{q}\) has external angles:

\[(.\overline{b_0 b_1 \ldots b_{q-3} 0 1}, .\overline{b_0 b_1 \ldots b_{q-3} 1 0})\]

where

\[b_0 b_1 \ldots = \operatorname{map} \left(\in \left(1 - \frac{p}{q}, 1\right)\right) \circ \operatorname{iterate} \left(+\frac{p}{q}\right) \$ \frac{p}{q}\]

Haskell Code

import Data.Fixed (mod')
import Data.List (genericTake)
import Data.Ratio (denominator)

type InternalAngle = Rational
type ExternalAngle = ([Bool], [Bool])

primaryBulb
  :: InternalAngle
  -> (ExternalAngle, ExternalAngle)
primaryBulb pq
  = ( ([], bs ++ [False, True])
    , ([], bs ++ [True, False])
    )
  where
    q = denominator pq
    bs
      = genericTake (q - 2)
      . map (\x -> 1 - pq < x && x < 1)
      . iterate (\x -> (x + pq) `mod'` 1)
      $ pq

Examples

Consider the bulb at internal angle \(\frac{p}{q} = \frac{2}{5}\):

\[\begin{aligned} r_0 = \frac{2}{5} &\not\in \left(1 - \frac{2}{5},1\right) &\therefore b_0 = 0 \\ r_1 = \frac{4}{5} & \in \left(1 - \frac{2}{5},1\right) &\therefore b_1 = 1 \\ r_2 = \frac{1}{5} &\not\in \left(1 - \frac{2}{5},1\right) &\therefore b_2 = 0 \end{aligned}\]

Therefore the external angles for the \(\frac{2}{5}\) bulb are:

\[\left( .\overline{01001}, .\overline{01010} \right)\]

The Farey Tree

Heiland-Allen (2016f)

Lavaurs' Algorithm

Heiland-Allen (2010d) Heiland-Allen (2010e)

Primary Hub

Primary Tips

Spoke Navigation

Heiland-Allen (2013b)

Islands in Hairs

Heiland-Allen (2013d) Heiland-Allen (2013e)

Hair Navigation

Heiland-Allen (2014d)

Other Angles

Heiland-Allen (2015a)

Further Algorithms

\[ \newcommand{\dd}[1]{\frac{\partial}{\partial{#1}}} \newcommand{\DD}[1]{\left\langle\!\!\!\left\langle#1\right\rangle\!\!\!\right\rangle} \newcommand{\SA}[1]{\left[\!\left[{#1}\right]\!\right]} \]

Perturbation

The idea

The shape of the Mandelbrot set is exceedingly intricate, with variety increasing the further we zoom in. Zooming in requires more precise numerical methods: we need at least enough information to distinguish nearby points in the region we want to visualize. Using this much information for each point is certainly good enough, but as the precision increases it gets slower.

The idea of perturbation (rediscoved independently by Martin (2013) and Khashin (2016)) is simple: take a high precision orbit for one point as a reference, and assuming a well-behaved function, the orbits for points near to the reference will for the most part be near to the reference orbit. Instead of computing nearby orbits at high precision, save time and effort by computing only the difference from the reference orbit.

This works out because if you have two high precision numbers close together, their difference has less meaningful precision. For example \[\begin{aligned} A &= 123456798 \\ B &= 123456789 \\ A - B &= 9 \end{aligned}\] even with \(A\) and \(B\) known to 9 significant figures, we can only determine their difference to 1 significant figure.

Applying the technique

Choose a reference \(c\) and iterate \(z\) (and its derivatives if needed) with high precision: \[\begin{aligned} z_0 &= z & z_{n+1} &= z_{n}^2 + c \\ \dd{z}z_0 &= 1 & \dd{z}z_{n+1} &= 2 z_{n} \dd{z}z_{n} \\ \dd{c}z_0 &= 0 & \dd{c}z_{n+1} &= 2 z_{n} \dd{c}z_{n} + 1 \\ \dd{z}\dd{z}z_0 &= 0 & \dd{z}\dd{z}z_{n+1} &= 2 z_{n} \dd{z}\dd{z}z_{n} + 2 {\dd{z}z_{n}}^2 \\ \dd{c}\dd{z}z_0 &= 0 & \dd{c}\dd{z}z_{n+1} &= 2 z_{n} \dd{c}\dd{z}z_{n} + 2 \dd{c}z_{n} \dd{z}z_{n} \end{aligned}\]

Define the deltas \(\DD{c},\DD{z},\ldots\) for a nearby orbit \(C,Z,\ldots\) which can be computed with lower precision: \[\begin{aligned} C &= c + \DD{c} \\ Z_{n} &= z_{n} + \DD{z_{n}} \\ \dd{z}Z_{n} &= \dd{z}z_{n} + \DD{\dd{z}z_{n}} \\ \dd{c}Z_{n} &= \dd{c}z_{n} + \DD{\dd{c}z_{n}} \\ \dd{z}\dd{z}Z_{n} &= \dd{z}\dd{z}z_{n} + \DD{\dd{z}\dd{z}z_{n}} \\ \dd{c}\dd{z}Z_{n} &= \dd{c}\dd{z}z_{n} + \DD{\dd{c}\dd{z}z_{n}} \end{aligned}\] Some boring algebraic manipulation gives the iterations for the deltas: \[\begin{aligned} \DD{z_{n+1}} &= 2 z_{n} \DD{z_{n}} + \DD{z_{n}}^2 + \DD{c} \\ \DD{\dd{z}z_{n+1}} &= 2 \left( \dd{z}z_{n} \DD{z_{n}} + z_{n} \DD{\dd{z}z_{n}} + \DD{z_{n}} \DD{\dd{z}z_{n}} \right) \\ \DD{\dd{c}z_{n+1}} &= 2 \left( \dd{c}z_{n} \DD{z_{n}} + z_{n} \DD{\dd{c}z_{n}} + \DD{z_{n}} \DD{\dd{c}z_{n}} \right) \\ \DD{\dd{z}\dd{z}z_{n+1}} &= 2 \left( \dd{z}\dd{z}z_{n} \DD{z_{n}} + z_{n} \DD{\dd{z}\dd{z}z_{n}} + 2 z_{n} \DD{\dd{z}z_{n}} \right. \\ & \quad + \left. \DD{z_{n}} \DD{\dd{z}\dd{z}z_{n}} + \DD{\dd{z}z_{n}}^2 \right) \\ \DD{\dd{c}\dd{z}z_{n+1}} &= 2 \left( \dd{c}\dd{z}z_{n} \DD{z_{n}} + z_{n} \DD{\dd{c}\dd{z}z_{n}} + \DD{z_{n}} \DD{\dd{c}\dd{z}z_{n}} \right. \\ & \quad + \left. \dd{c}z_{n} \DD{\dd{z}z_{n}} + \DD{\dd{c}z_{n}} \dd{z}z_{n} + \DD{\dd{c}z_{n}} \DD{\dd{z}z_{n}} \right) \end{aligned}\] For interior coordinates and interior distance estimation, we need to solve \(Z_p = Z_0\), but when \(z_p = z_0\) we can apply the perturbation technique to Newton's method for root finding: \[\begin{aligned} Z_0^{(m+1)} &= Z_0^{(m)} - \frac{Z_p^{(m)} - Z_0^{(m)}}{\dd{z}Z_p^{(m)} - 1} \\ \DD{z_0}^{(m+1)} &= \DD{z_0}^{(m)} - \frac{\DD{z_p}^{(m)} - \DD{z_0}^{(m)}}{\dd{z}{z_p} + \DD{\dd{z}{z_p}}^{(m)} - 1} \end{aligned}\] The precondition isn't too onerous, as it's often sensible to choose a periodic point as a reference, and it's enough if \(p\) is a multiple of the period of the reference.

Glitch Correction

Heiland-Allen (2014a)

Series Approximation

The perturbed deltas are polynomial series in \(\DD{c}\). Define the coeffecients \(\SA{z_n}_m,\SA{\dd{c}z_n}_m\) of the polynomials for each delta: \[\begin{aligned} \DD{z_n} &= \sum \SA{z_n}_m \DD{c}^m & \DD{\dd{c}z_n} &= \sum \SA{\dd{c}z_n}_m \DD{c}^m \\ \end{aligned}\] Some boring algebraic manipulation gives the iterations for the first few coefficients of \(\DD{z_n}\): \[\begin{aligned} \SA{z_{n+1}}_1 &= 2 z_n \SA{z_n}_1 + 1 \\ \SA{z_{n+1}}_2 &= 2 z_n \SA{z_n}_2 + \SA{z_n}_1^2 \\ \SA{z_{n+1}}_3 &= 2 z_n \SA{z_n}_3 + 2 \SA{z_n}_1 \SA{z_n}_2 \\ \end{aligned}\] and similarly for the coefficients of \(\DD{\dd{c}z_n}\): \[\begin{aligned} \SA{\dd{c}z_{n+1}}_1 &= 2 \left( \dd{c}z_n \SA{z_n}_1 + z_n \SA{\dd{c}z_n}_1 \right) \\ \SA{\dd{c}z_{n+1}}_2 &= 2 \left( \dd{c}z_n \SA{z_n}_2 + z_n \SA{\dd{c}z_n}_2 + \SA{z_n}_1 \SA{\dd{c}z_n}_1 \right) \\ \SA{\dd{c}z_{n+1}}_3 &= 2 \left( \dd{c}z_n \SA{z_n}_3 + z_n \SA{\dd{c}z_n}_3 + \SA{z_n}_1 \SA{\dd{c}z_n}_2 + \SA{z_n}_2 \SA{\dd{c}z_n}_1 \right) \end{aligned}\] The coefficients are independent of \(\DD{c}\) so the same coefficients can be used for many points in an image, and when \(|\DD{c}|\) is small the sum can be approximated by truncating to the first few terms. However, the coefficients grow quickly as \(n\) increases, which limits how long the per-reference approximation remains valid, after which we have to switch back to per-point delta iteration.

See Martin (2013), Heiland-Allen (2016d), Heiland-Allen (2016b).

Zoom Interpolation

Heiland-Allen (2010a)

Poincaré Zoom

Heiland-Allen (2011)

Exponential Map

Heiland-Allen (2010f) Heiland-Allen (2014g)

Moebius Warp

Heiland-Allen (2013g)

Julia Morphing

Heiland-Allen (2015d) Heiland-Allen (2016a) Heiland-Allen (2016c)

Buddhabrot

Heiland-Allen (2013h) Heiland-Allen (2016e)

Spider Algorithm

Heiland-Allen (2014b)

Bibliography