Automated Julia morphing
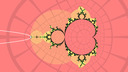
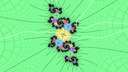
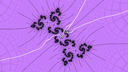
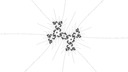
In a previous post I described a way to sculpt patterns in the Mandelbrot set, noting that I hoped to automate it in the future. This week I finally got around to it. The first 5 images in the gallery below show the first few stages of a Julia morphing sequence, with some periods annotated and external rays drawn on. I derived the external angles from periodic truncation at the relevant period of the bit sequence given by tracing external rays outwards towards infinity.
The external angles are:
period 5 .(01111) .(10000) period 54 .(011111000001111100000111110000011111000001111011111000) .(011111000001111100000111110000011111000001111100000111) period 69 .(011111000001111100000111110000011111000001111011111000011111000010000) .(011111000001111100000111110000011111000001111011111000100000111101111) period 143 .(01111100000111110000011111000001111100000111101111100010000011110111101111100000111110000011111000001111100000111101111100001111100001000010000) .(01111100000111110000011111000001111100000111101111100010000011110111101111100000111110000011111000001111100000111101111100010000011110111101111) .period 291 .(011111000001111100000111110000011111000001111011111000100000111101111011111000001111100000111110000011111000001111011111000100000111101111011110111110000011111000001111100000111110000011110111110001000001111011110111110000011111000001111100000111110000011110111110000111110000100001000010000) .(011111000001111100000111110000011111000001111011111000100000111101111011111000001111100000111110000011111000001111011111000100000111101111011110111110000011111000001111100000111110000011110111110001000001111011110111110000011111000001111100000111110000011110111110001000001111011110111101111)
Letting the period 5 angles be .(a) and .(b), and the period 69 angles be .(A) and .(B), the period 143 angles can be written .(C) = .(BAb) and .(D) = .(BBa), and moreover the period 291 angles are then .(DCb) and .(DDa) - this suggests a pattern which could be extrapolated, and indeed repeating this concatenation process seems to work as the last 8 images in the gallery above show.
However tracing the external rays to a sufficient depth that Newton's method iterations can find the correct periodic nucleus is asymptotically \(O(p^2)\) for period \(p\), and the period is more than doubled each step, so the runtime increases by a factor of more than 4 for each successive location in the sequence. This makes it far too slow to be practical - it's much quicker to do the zooming and point selection by hand/eye (the last in the sequence in the gallery took over 24 hours just to find the location on my machine, dwarfing the time needed to render the actual image).
Here's the core of the code used to render the final sequence, using my mandelbrot-numerics and mandelbrot-symbolics libraries to calculate viewing parameters, and mandelbrot-perturbator to render the images. I need to turn the bin/glfw3.c of the latter project into a reusable library too, because the full program is pretty much the same minus input handling etc.
...
extern int main(int argc, char **argv) {
...
// initialize Julia morphing state
int sharpness = 8;
m_block a, b;
m_block_init(&a);
m_block_init(&b);
m_block_from_string(&a, "01111");
m_block_from_string(&b, "10000");
m_binangle as[2], bs[2];
m_binangle_init(&as[0]);
m_binangle_init(&bs[0]);
m_binangle_from_string(&as[0], ".(011111000001111100000111110000011111000001111011111000011111000010000)");
m_binangle_from_string(&bs[0], ".(011111000001111100000111110000011111000001111011111000100000111101111)");
m_binangle_init(&as[1]);
m_binangle_init(&bs[1]);
mpq_t q;
mpq_init(q);
mpc_t c[2], delta;
mpc_init2(c[0], 53);
mpc_init2(c[1], 53);
mpc_init2(delta, 53);
// create renderer
struct perturbator *context = perturbator_new(workers, width, height, maxiters, chunk, escape_radius, glitch_threshold);
for (int depth = 0; depth < 20; ++depth) {
// poll GUI for quit event
glfwPollEvents();
if (glfwWindowShouldClose(window)) {
break;
}
// trace external ray to nucleus
int w = (depth + 1) & 1;
m_binangle_to_rational(q, &as[1 - w]);
m_r_exray_in *ray = m_r_exray_in_new(q, sharpness);
for (int s = 0; s < 2 * as[1 - w].per.length * sharpness; ++s) {
m_r_exray_in_step(ray);
}
m_r_exray_in_get(ray, c[1 - w]);
m_r_nucleus(c[1 - w], c[1 - w], as[1 - w].per.length, 64);
if (depth > 0) {
// compute view from two nuclei in the embedded Julia set
mpc_sub(delta, c[w], c[1 - w], MPC_RNDNN);
mpc_abs(state.radius, delta, MPFR_RNDN);
mpfr_mul_d(state.radius, state.radius, 12, MPFR_RNDN);
mpfr_set_prec(state.centerx, mpc_get_prec(c[w]));
mpfr_set_prec(state.centery, mpc_get_prec(c[w]));
mpfr_set(state.centerx, mpc_realref(c[w]), MPFR_RNDN);
mpfr_set(state.centery, mpc_imagref(c[w]), MPFR_RNDN);
// render raw data and wait for it to complete
perturbator_start(context, state.centerx, state.centery, state.radius);
perturbator_stop(context, false);
// refresh image and save to PPM file
glTexSubImage2D(GL_TEXTURE_2D, 0, 0, 0, width, height, GL_RGBA, GL_FLOAT, perturbator_get_output(context));
refresh_callback(&state);
glReadPixels(0, 0, width, height, GL_RGB, GL_UNSIGNED_BYTE, ppm);
printf("P6\n%d %d\n255\n", width, height);
for (int y = height - 1; y >= 0; --y) {
fwrite(ppm + y * width * 3, width * 3, 1, stdout);
}
fflush(stdout);
}
// extrapolate next external angle pair
m_block_append(&as[w].per, &bs[1-w].per, &as[1-w].per);
m_block_append(&as[w].per, &as[w].per, &b);
m_block_append(&bs[w].per, &bs[1-w].per, &bs[1-w].per);
m_block_append(&bs[w].per, &bs[w].per, &a);
}
...
}You can download the full automated julia morphing example code which you can drop into a mandelbrot-perturbator git clone bin/ directory and compile with the hints at the top of the file.
At some point I'll try a hybrid approach that mimics more closely the hand/eye method, approximating the zoom depth needed for each successive morph and using just the pattern of periods with Newton's method to find the next nucleus, but it might find the "wrong" nucleus which is quite likely due to symmetry and there is a chance it might go way off...
In summary: this automated Julia morphing works in theory, but it's not practical computationally.