mathr / blog / #

Generating deep zoom images of the Mandelbrot set by iterations of \( z_{n+1} = F(z_n, c) \) require high precision for \(z_n\) and \(c\). Perturbation techniques use a high precision reference with low precision deltas which I write \( \left<\left< . \right>\right> \):

\[ z_{n+1} + \left<\left< z_{n+1} \right>\right> \gets F\left( z_n + \left<\left< z_n \right>\right> , c + \left<\left< c \right>\right> \right) \]

Boring algebraic manipulation gives the perturbed iteration equation:

\[ \left<\left< z_{n+1} \right>\right> \gets \left<\left< F \right>\right> \left(z_n, \left<\left< z_n \right>\right>, \left<\left< c \right>\right> \right) \]

Series approximation techniques assume \( \left<\left< z_n \right>\right> \) can be expressed in terms of \( \left<\left< c \right>\right> \):

\[ \left<\left< z_n \right>\right> = \sum_{k=1}^\infty{a_{k,n} {\left<\left< c \right>\right>}^k} \]

Substituting the series expression for \( \left<\left< z_n \right>\right> \) into the right hand side of the perturbed iteration equation and collecting terms by powers of \( \left<\left< c \right>\right> \) gives a collection of iteration equations for the coefficients \( a_k \):

\[ a_{k, n + 1} = A_k \left( z_n , \left\{ a_{j,n} : j \le k \right\} \right) \]

These recurrence relations are in complex variables, but arbitrary precision arithmetic libraries like MPFR generally work with real variables, so more boring algebraic manipulation expands each recurrence into a pair of recurrences involving the real and imaginary parts.

The functions in libraries like MPFR are quite basic - typically they take two input variables and an output variable, and compute a single arithmetic operation. Modern CPUs (and GPUs) have many cores, and systems like OpenMP allow to parallelize code to utilize more than one core. Parallel loops perform the same operation multiple times (compare with SIMD), but the recurrence expressions are mixed up mash of operations. So I canonicalize the recurrences into a representation that allows to extract as much uniform-operation parallelism as possible.

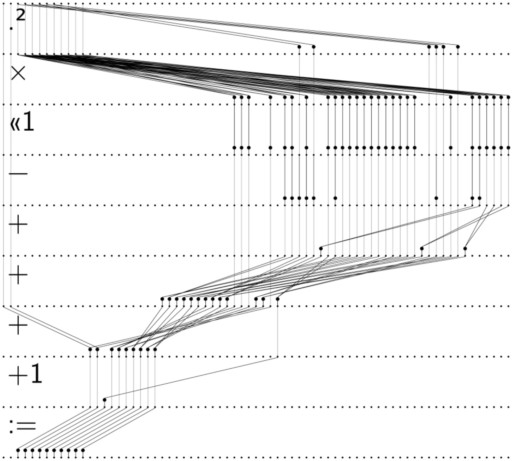
The outer-most operation is a sum, with each term being a product of a small integer with another sum. Each inner sum term is an optional negation of an optional scaling by a power of two of a product of powers. Negation and scaling by a power of two are very cheap operations. Squaring a high precision real number is cheaper than multiplying two different numbers, so powers are factored to use as much squaring as possible.

The computations are split into a sequence of phases, with each phase performing a parallel operation. The first phases compute all the squarings that are necessary for the powers. The next phases perform all the non-squaring products. The product (or sum) of a number of terms can be performed partially in parallel by careful bracketing: a * b * c * d becomes (a * b) * (c * d) with the two inner products performed in parallel before the outer product. Here's a diagram for an order 4 series:

The code generator is implemented in Haskell, and outputs C code using MPFR and OpenMP. You can find it as part of my (still-experimental) mandelbrot-perturbator project. The Haskell is really very ugly though (lots of dirty String concatenation to emit C code), not to mention inefficient - expect high order series to take a vast amount of time. The generator theoretically supports arbitrary integer powers in \(z \to z^p+c\) but I've only tested with \(p = 2\) because the rest of the perturbator code (mostly C-style C++ with a few templates and overloaded numerics) hasn't got some needed functionality for other powers. Eventually I plan to extend the code generator to emit the missing pieces, but first I want to experiment with native precision operations for some coefficients in the hope that it isn't so deathly slow for high order series at very deep zooms. Currently rendering a (boring) test zoom, only 400 frames away from 1e-10000. It's taking a while though, might be done by May.

Note: most of this post was written in May last year, the generator probably changed a bit since then.