Stretching cusps
Figure 4.22 on pages 204-205 of The Science Of Fractal Images is presented with this description:
A region along the cardioid is continuously blown up and stretched out, so that the respective segment of the cardioid becomes a line segment. ... Our blow-up factor is chosen accordingly to the result that all disks in Figure 4.22 have the same size.
While waiting for a train the other day, I remembered this image, and wanted to recreate it, which required deriving the equations (they were not presented in the book).
A Möbius transformation of the complex plane is a rational function of the form
\[ f(z) = \frac{a z + b}{c z + d} \]
with \( a d − b c \ne 0 \). It has inverse
\[ f^{-1}(z) = \frac{d z - b}{-c z + a} \]
Möbius transformations are conformal, preserving angles but not lengths, and map generalized circles to generalized circles (generalized circles include lines as the special case of a circle through infinity). A Möbius transformation can be constructed from 3 points and their images. For our purposes, we can choose the images of \(P_0, P_1, P_\infty\) to be \(0, 1, \infty\), which gives
\[ F(z) = \frac {(z-P_0)(P_1-P_\infty)}{(z-P_\infty)(P_1-P_0)} \]
This \(F\) stretches and flattens a circle through \(P_0, P_1, P_\infty\) into a straight line, with the blow-up factor increasing towards \(\infty\). If \(P_\infty\) is chosen as a cusp, all the primary discs along the path to the cusp get stretched to be roughly the same size.
So far this works for circles, but cardioids require another conformal map to transform them into circles so that the Möbius transformation can work its magic. A cardioid with its cusp at \(0\) and its front at \(4\) is transformed into a unit circle centered at \(1\) by \(f(z) = \sqrt{z}\) (with the branch cut of the square root along the negative real axis). So to transform the period 1 cardioid of the Mandelbrot set (which has cusp at \(1/4\) and front at \(-3/4\)) to a unit circle centered at \(0\) the resulting conformal map is
\[ G(z) = \sqrt{1 - 4 z} - 1 \]
with inverse
\[ G^{-1}(z) = \frac{1 - (z+1)^2}{4} \]
Now, given \(P_0, P_1, P_\infty\) on the cardioid, form the Möbius transformation \(F\) for \(G(P_0), G(P_1), G(P_\infty)\), then \(F(G(c))\) maps \(c\) near the boundary of the Mandelbrot set cardioid to a flattened strip near the real axis. But when rendering images, we start from a rectangle with coordinates \([0..\text{width})\times[0..\text{height})\), so we have to work backwards to find the corresponding \(c\) in the parameter plane. Inverting \(k = F(G(c))\) gives \(G^{-1}(F^{-1}(k)) = c\).
Moreover, for distance estimation colouring it's useful to colour pixels according to the distance estimate relative to the pixel spacing, which is no longer fixed when applying a conformal mapping with non-constant scaling. The scale factor associated with a conformal mapping is the absolute value of its derivative, and the relevant derivatives are
\[ \begin{aligned} \frac{\partial}{\partial z} \frac{a z + b}{c z + d} &= \frac{a d - b c}{(c z + d)^2} \\ \frac{\partial}{\partial z} \frac{1 - (z+1)^2}{4} &= \frac{-(z+1)}{2} \\ \frac{\partial}{\partial z} f(g(z)) &= \frac{\partial f}{\partial z}(g(z)) \frac{\partial g}{\partial z}(z) \end{aligned} \]
The third equation is the chain rule for derivative of function composition, which can be intuitively expressed as "multiply all the derivatives at each step".
Putting together all the transformations and their derivatives and choosing the preimages \(P_0, P_1, P_\infty\) as bond points and cusps on the boundary of the Mandelbrot set, gives some stretched cusp pictures.
Map of strip locations.
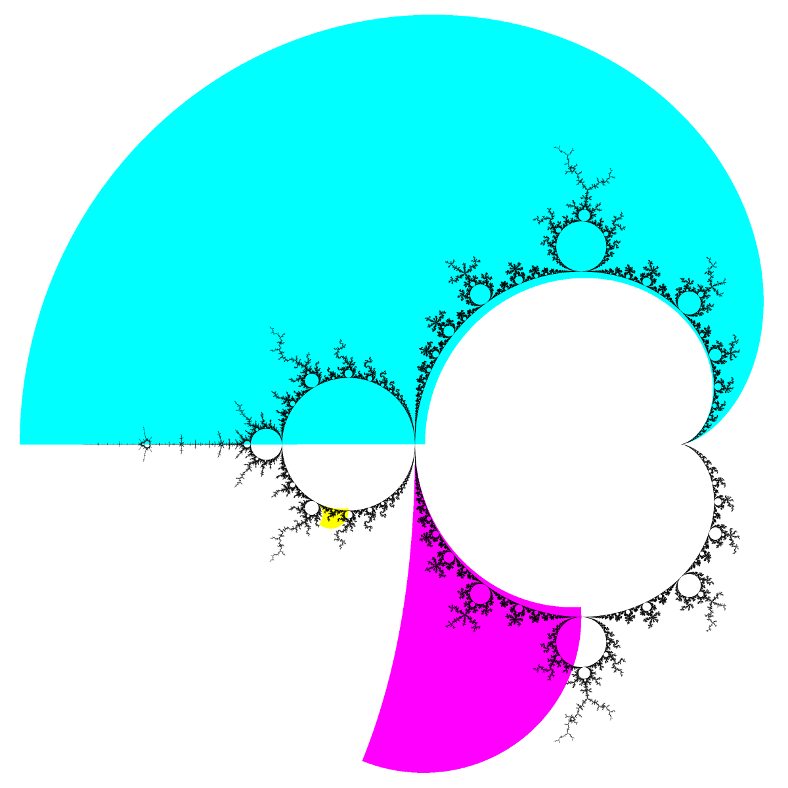
Elephant valley (cyan).

Seahorse valley (magenta).

"Double rabbit valley" (yellow).
