mathr / blog / #

(skip to conclusions and music video link)

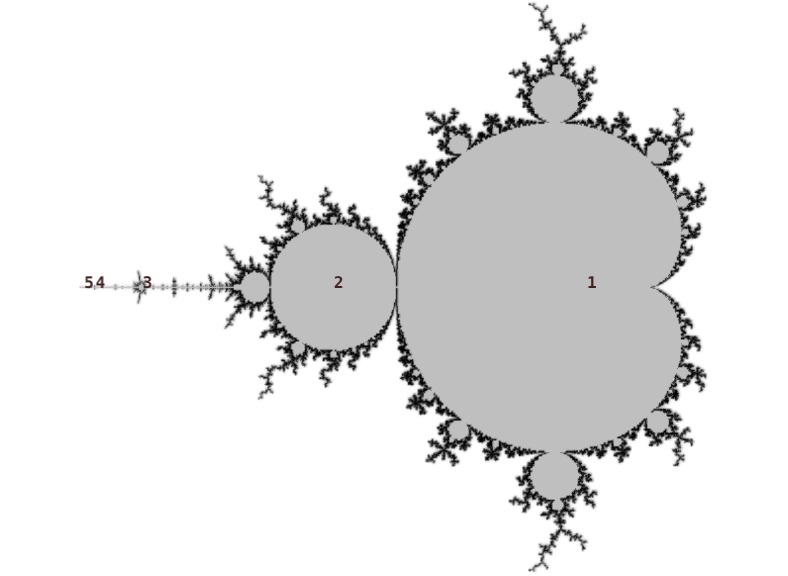
In this post I'll be using the west-most period 5 island as an example, but the patterns also occur for some (most? all?) other islands. The island has angled internal address 1 1/2 2 1/2 3 1/2 4 1/2 5.

Getting close to the island some hairs are visible. The lowest period islands in each hair are near the tip: see the period 11 marked at the top and bottom of the following image. These periods also occur in the longer hairs (the 11 marked at left and right). Going deeper to the next layer of hairs, the lowest period in the inner hairs is 16.

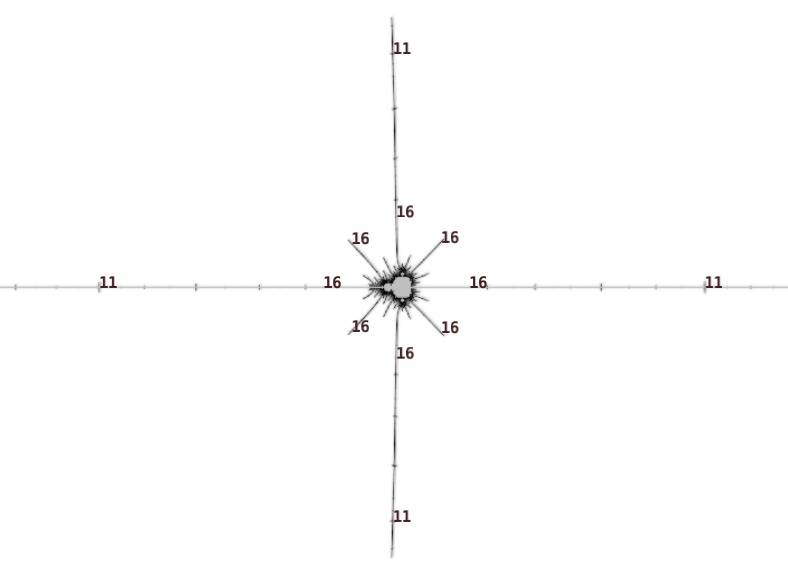
The sequence 11, 16, 21, 26, ... increases by 5 at each level of hairs. The period of the inner atom is 5.

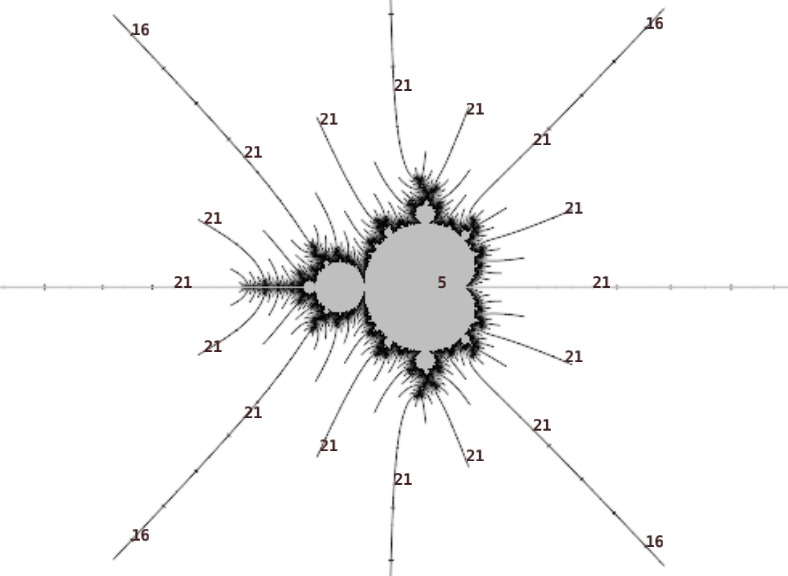
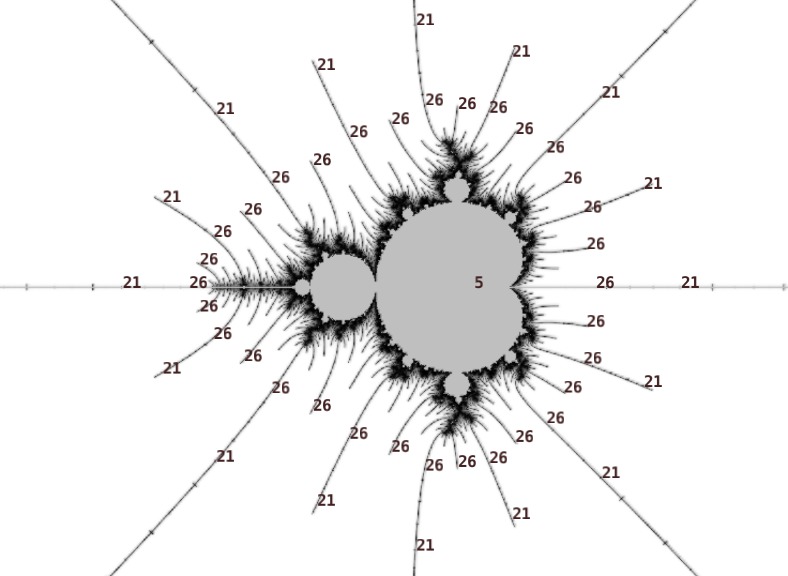
This pattern continues indefinitely. But what of the structure around each of those islands? I'll use a period 131 island in the positive cusp of the 1/3 bulb of the period 5 island as an example, but the patterns also occur for some (most? all?) other low period islands in the hairs.

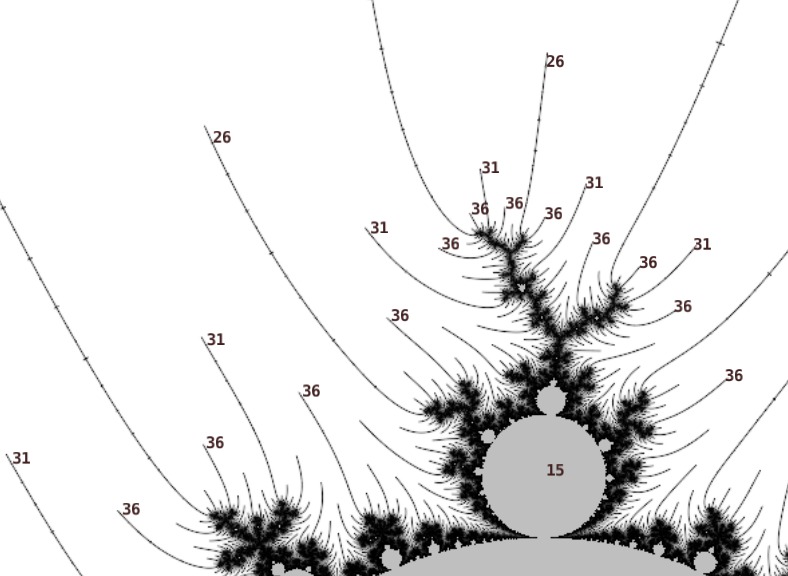
Getting closer to the island there is an embedded Julia set. The periods in the hairs outside the embedded Julia set also increase by 5.

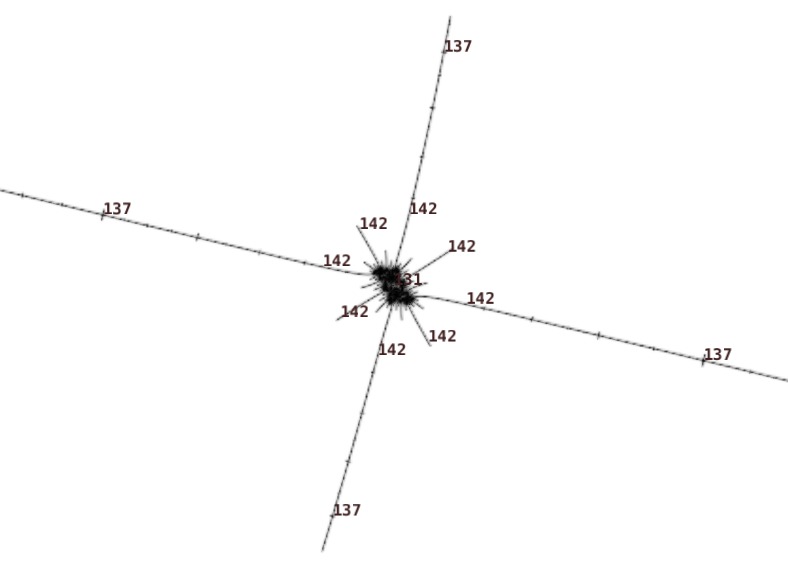
Within the embedded Julia set, periods also increase in steps of 5. Moving outwards towards the tips, the periods increase by 5: 131, 136, 141, 146, 151, ... Rotating clockwise about a spiral, the periods increase by 5: 136, 141, 146, ... Moving inwards along a spiral is the same as rotating 3 times (for the 3 spokes) and the periods increase by 15: 136, 151, 166, ...

Going deeper into the embedded Julia set, at the next level the periods increase by 131 relative to the outer level: 136 + 131 = 267, etc...

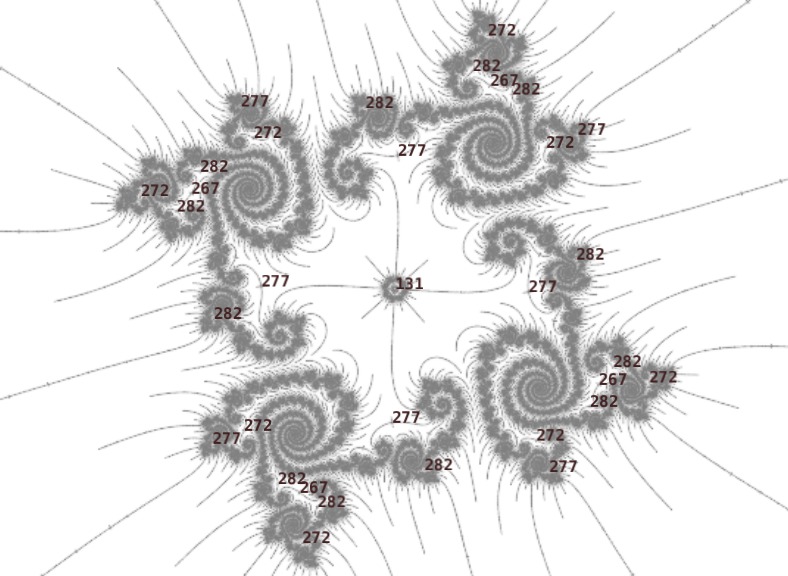
Going deeper into the embedded Julia set, at the next level the periods increase by 131 relative to the outer level: 267 + 131 = 398, etc...

The pattern seems to be:

outer period P

(example: 5)

inner period Q at offset K and depth N (giving 2^N islands)

Q = N * P + K

embedded Julia set period J at depth M (giving 2^M-fold symmetry)

J = P + M * Q

So our period 131 island has P = 5, Q = 131, K = 1, N = 26. The 2-fold embdedded Julia set has period 5 + 131 = 136; 4-fold, 5 + 2 * 131 = 267; 8-fold, 5 + 3 * 131 = 398; 16-fold, 529; ...

In a future post I'll describe some patterns in the external angles of these islands in the hairs and embedded Julia sets, which allows for the creation of non-standard (by which I mean not just a continuous zoom) Mandelbrot set videos. Here's one I prepared earlier: Hairy Julias.