mathr / blog / #

I've been working on a Mandelbrot set explorer program, but it's slow: it doesn't (yet) use the perturbation techniques and its series approximation extension which allow lower-precision calculations for the bulk of the work. There are a few renderers out there which implement the optimisation:

• SuperFractalThing the original program by K I Martin that popularized the technique, cross-platform Java.
• Kalles Fraktaler by Karl Runmo, Windows C++ 32bit and 64bit, but the 32bit version works on Linux with wine32.
• Mandel Machine by Botond Kósa, Windows Java C++ and ASM, 64bit only. Supposedly the fastest, but I haven't got a working wine64 so haven't tried it yet.

Source code for all three is available, and both Kalles Fraktaler and Mandel Machine can save the raw iteration data for later colouring or other analysis. Kalles Fraktaler can render videos as keyframes at 2-fold zoom out, and I've had some success colourizing this raw data and assembling the resulting images into videos using a program I described in 2010 in Optimizing zoom animations.

I have an aesthetic preference for distance estimate colouring - I think it looks better, and it's also arguably a more accurate representation of the structure of the Mandelbrot set: every dark pixel is near the boundary of the set and every pixel near the boundary of the set is dark. However, none of the three programs I mentioned calculate the derivatives needed to calculate the exterior distance estimate, let alone the interior distance estimate.

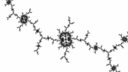
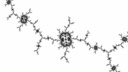
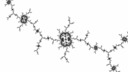
A few recent threads at Fractal Forums (search for "bump mapping") inspired me to try out a variation: I had an idea to change the hue based on the slope angle, instead of a lighting effect. My first attempt was a bit grungy but swapping the value gradient worked a lot better - and it looked a bit like distance estimate colouring! The dark boundary was clearly visible in the image. I tweaked my colouring program to use a monochrome palette and rendered some raw images in Kalles Fraktaler:

The leftmost ones look pretty ugly, but supersampling (rendering and colouring a larger image and then downscaling) makes the later ones in each row look almost as good as true distance estimate rendering. I added rainbow slope colourings for each as a bonus (mainly to align the rows).

You can download the C99 source code tarball that coloured the images (calculated with Kalles Fraktaler) in this post. Both programs take .kfb input on stdin, and output pgm (pseudo-de) or ppm (rainbow) on stdout (so redirect it for best results).