mathr / blog / #

The external angles of the period 3 island are \(.(011)\) and \(.(100)\). The period 65 island in the longest hair of the \(7/8\) child of the \(1/3\) child of the period 3 island has external angles:

\(.(01110001101110001101110001101110001101110001101110001101101110010)\)

\(.(01110001101110001101110001101110001101110001101110001101110001101)\)

Call these repeated blocks of 65 digits \(p_{65}\) and \(P_{65}\) with \(p_{3}\) and \(P_{3}\) for the length 3 blocks of the influencing island.

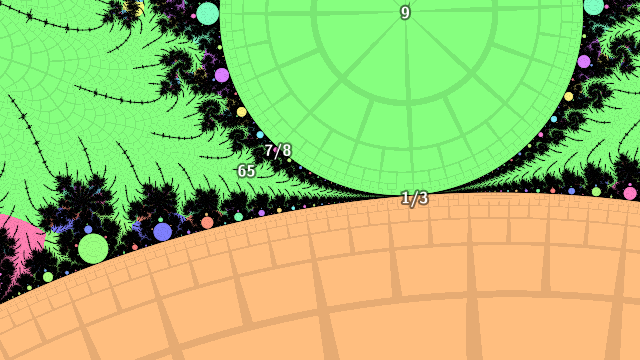
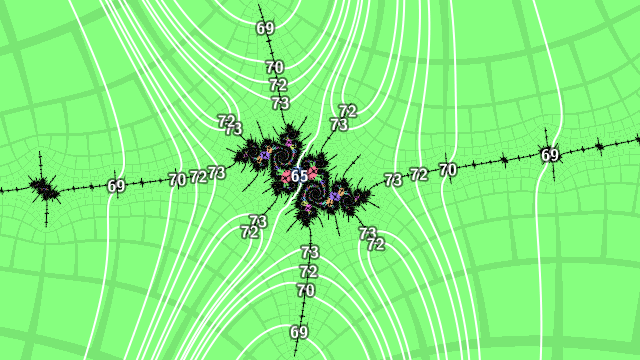
Then the external angles landing at the period 69 islands in the hairs are

\[\begin{aligned} .(p_{65} p_{3} 0) \\ .(p_{65} p_{3} 1) \\ .(p_{65} P_{3} 0) \\ .(p_{65} P_{3} 1) \\ .(P_{65} p_{3} 0) \\ .(P_{65} p_{3} 1) \\ .(P_{65} P_{3} 0) \\ .(P_{65} P_{3} 1) \end{aligned}\]

and the external angles landing at the period 70 islands in the hairs are

\[\begin{aligned} .(p_{65} p_{3} 01) \\ .(p_{65} p_{3} 10) \\ .(p_{65} P_{3} 01) \\ .(p_{65} P_{3} 10) \\ .(P_{65} p_{3} 01) \\ .(P_{65} p_{3} 10) \\ .(P_{65} P_{3} 01) \\ .(P_{65} P_{3} 10) \end{aligned}\]

The rays land in pairs: the first and last in each list are a pair, then neighbours in the inner bulk (the 2nd and 3rd form a pair, so do the 4th and 5th, etc). Going in a level along the hairs, the period 72 islands have external angles

\[\begin{aligned} .(p_{65} p_{3} p_{3} 0) \\ .(p_{65} p_{3} p_{3} 1) \\ .(p_{65} p_{3} P_{3} 0) \\ .(p_{65} p_{3} P_{3} 1) \\ .(p_{65} P_{3} p_{3} 0) \\ .(p_{65} P_{3} p_{3} 1) \\ .(p_{65} P_{3} P_{3} 0) \\ .(p_{65} P_{3} P_{3} 1) \\ .(P_{65} p_{3} p_{3} 0) \\ .(P_{65} p_{3} p_{3} 1) \\ .(P_{65} p_{3} P_{3} 0) \\ .(P_{65} p_{3} P_{3} 1) \\ .(P_{65} P_{3} p_{3} 0) \\ .(P_{65} P_{3} p_{3} 1) \\ .(P_{65} P_{3} P_{3} 0) \\ .(P_{65} P_{3} P_{3} 1) \end{aligned}\]

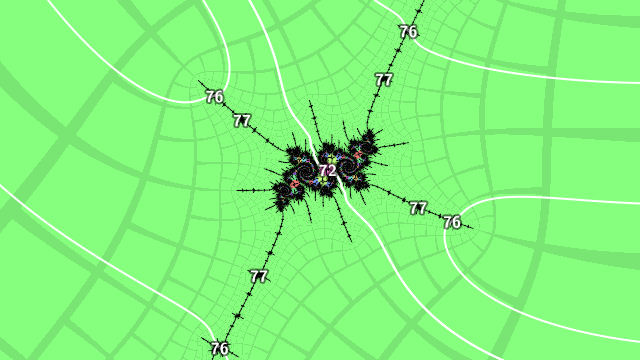
Picking one of these period 72 islands with external angles \(.(p_{72}) = .(P_{65} p_{3} p_{3} 1)\) and \(.(P_{72}) = .(P_{65} p_{3} P_{3} 0)\), the period 76 islands nearby have external angles

\[\begin{aligned} .(p_{72} p_{3} 0) \\ .(p_{72} p_{3} 1) \\ .(p_{72} P_{3} 0) \\ .(p_{72} P_{3} 1) \\ .(P_{72} p_{3} 0) \\ .(P_{72} p_{3} 1) \\ .(P_{72} P_{3} 0) \\ .(P_{72} P_{3} 1) \end{aligned}\]

These patterns are essentially counting in binary, with the bits mapped to segments of different lengths. The least significant bit is just copied, the most significant bit determines which block from the inner island is used, and the bits in between use blocks from the influencing island (here of period 3).

In 2011 I made a video zooming close to a sequence of embedded Julia sets before hopping inside. With the patterns elaborated on in this post I rendered a new video, taking a more analytical approach - zooming close to the embedded Julia sets in a circuit around the set instead of navigating by hand. I wrote a little Haskell code to implement this idea:

import Data.Bits (testBit)

base :: (String, String)
base =( "01110001101110001101110001101110001101110001101110001101101110010"
      , "01110001101110001101110001101110001101110001101110001101110001101"
      )

binary :: Int -> Integer -> [Bool]
binary digits n = [ testBit n b | b <- [digits-1,digits-2..0] ]

step :: Int -> ((String, String), Integer) -> ((String, String), Integer)
step depth ((blo, bhi), index) = ((b0++g0++i0, b1++g1++i1), index + 4)
  where
    lo = binary depth index
    hi = binary depth (index + 1)
    b0 = if head lo then bhi else blo
    i0 = if last lo then "1" else "0"
    g0 = concat [ if g then "100" else "011" | g <- tail (init lo) ]
    b1 = if head hi then bhi else blo
    i1 = if last hi then "1" else "0"
    g1 = concat [ if g then "100" else "011" | g <- tail (init hi) ]

main :: IO ()
main = print $ iterate (step 6) (base, 1) !! 16

I traced an external ray from the output of period 273 to give the coordinates of the zoom center.

You can watch the original 2011 video on the Internet Archive, I'll upload the high resolution version of the 2014 reimagining to the same link just as soon as it's finished rendering, meanwhile here's a lofi preview.