A ball bouncing down steps
The first part of the process is a ball in free flight from one step down to the next:
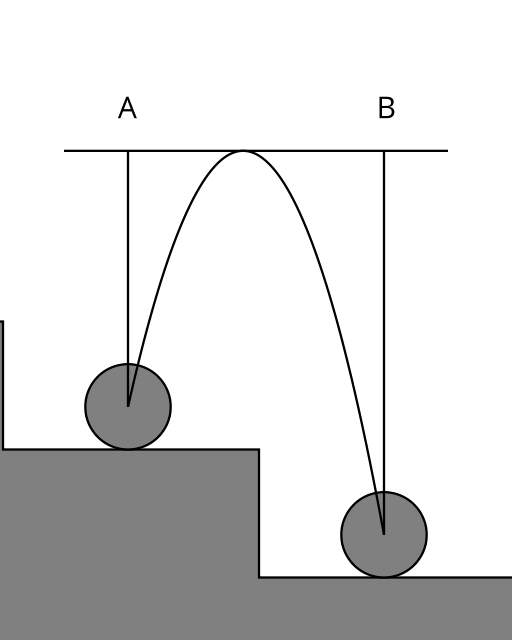
Consider gravitational potential energy \(m g h\) (where m is mass, g is the force of gravity, and h is the height) at the peak height \(H\) of the flight path over steps of height \(S\) relative to A and B:
\[\begin{aligned} E_A &= m g (H - S) \\ E_B &= m g H \end{aligned}\]
Consider kinetic energy \(\frac{1}{2} m v^2 \) at A and B:
\[\begin{aligned} E_A &= \frac{1}{2} m v_A^2 \\ E_B &= \frac{1}{2} m v_B^2 \end{aligned}\]
Some simple algebra gives:
\[\begin{aligned} v_A = \sqrt{ 2 g (H - S) } \\ v_B = \sqrt{ 2 g H } \end{aligned}\]
When in flight, the only force acting on the ball is gravity. Using Newton's law of motion relating force and acceleration \(F = m a\) and integrating with the initial conditions at \(A\) with \(t = 0\) gives:
\[\begin{aligned}\frac{\partial}{\partial t}\frac{\partial}{\partial t} y & = -g \\ \frac{\partial}{\partial t} y &= v_A - g t \\ y &= r + v_A t - \frac{1}{2} g t^2 \end{aligned} \]
where \(y\) is the height of the ball center and \(r\) is the ball radius. Now we can find the duration \(T_f\) of the flight, which ends when \(y(T_f) = y(0) - S\):
\[\begin{aligned} r - S &= r + v_A T_f - \frac{1}{2} g T_f^2 \\ \frac{1}{2} g T_f^2 - v_A T_f - S &= 0 \\ T_f = \frac{v_A + \sqrt{ v_A^2 + 2 g S } }{ g } \end{aligned}\]
The second part of the process is a compressive bounce when the ball reaches the lower step:
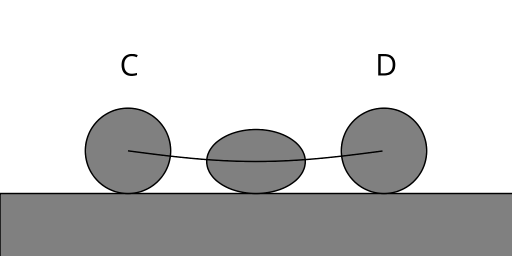
Modelling the bounce by a damped harmonic oscillator gives an equation of motion, where \(d\) is the maximal squashing of the ball:
\[y = r \left( 1 - d \sin (\beta t) e^{-\gamma t} \right)\]
Here \(\beta\) determines the speed of the bounce and \(\gamma\) determines the energy lost during the bounce. Using the boundary conditions \(v_C = v_B\) and \(v_D = v_A\) for a smooth transition from free flight to bouncing, and setting \(T_b\) to be the duration of the bounce (time of first return to initial \(y\) value), we can differentiate the equation of motion and solve for the unknowns:
\[ \begin{aligned} \frac{\partial}{\partial t} y &= r e^{-\gamma t} \left( \gamma \sin(\beta t) - d \beta \cos(\beta t) \right) \\ v_B &= r d \beta \\ \beta &= \frac{v_B}{r d} \\ T_b &= \frac{\pi}{\beta} \\ v_A &= r e^{-\gamma T_b} d \beta \\ \gamma &= -\frac{\log \frac{v_A}{r d \beta}}{T_b} \end{aligned} \]
The time taken for the whole loop is \(T = T_f + T_b\). Assuming the ball is initially spherical, and that volume remains constant, we can compute the squashing factor using the property of an ellipsoid that \(V = k r_x r_y r_z\) assuming that \(r_x = r_z\):
\[ \begin{aligned} r_y &= y \\ r_x &= \sqrt{\frac{r^3}{y}} \end{aligned} \]
Implementing all these equations in the Haskell programming language using the Diagrams library for visualization gives some cute animated GIFs:
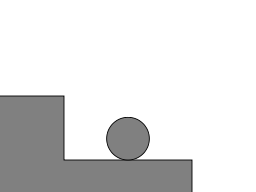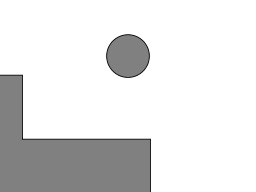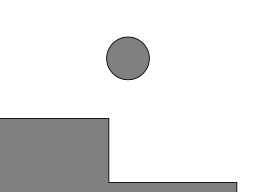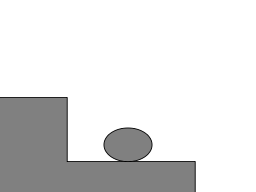
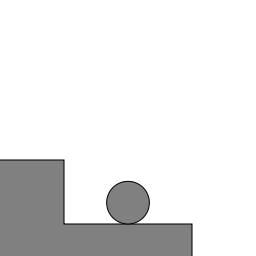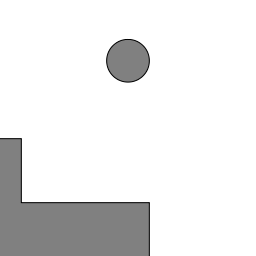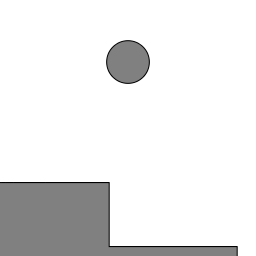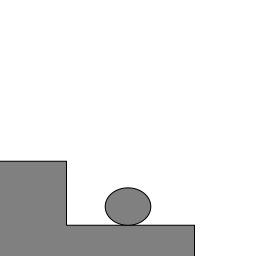
You can download the full source code for this post.