mathr / blog / #

I've been meaning to try Fluxus for some time, and finally got around to it at the weekend. I initially jumped in at the deep end, trying to implement hypercube rendering, but I quickly realized I need to learn more about Scheme/Guile/OpenGL/Fluxus before I would be able to achieve it.

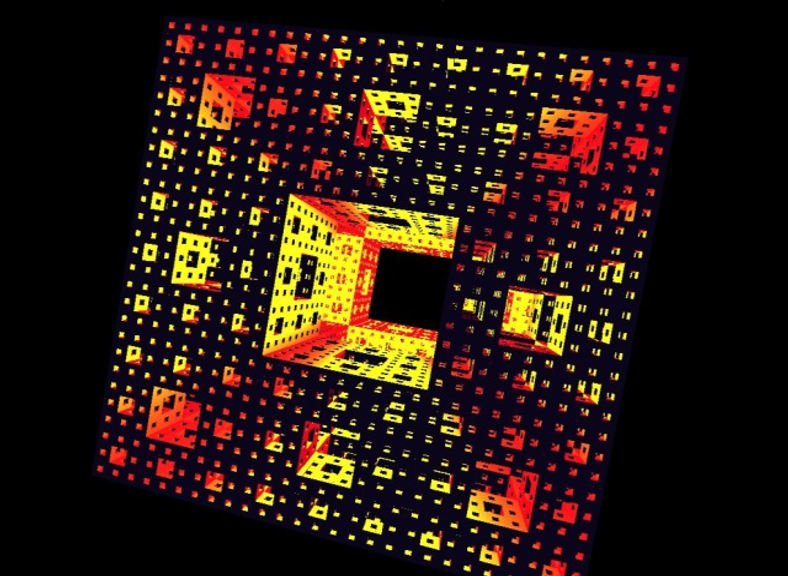
The first non-trivial thingy I made was a Menger Sponge:

(save-name "menger-sponge.scm")

(define (build-sponge n o)
    (push)
    (if (< n 1)
        (begin
            (o)
        )
        (begin
            (scale (vector (/ 1 3) (/ 1 3) (/ 1 3)))
            (push) (translate (vector -1 -1 -1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector -1 -1  0)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector -1 -1  1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector -1  0 -1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector -1  0  1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector -1  1 -1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector -1  1  0)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector -1  1  1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector  0 -1 -1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector  0 -1  1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector  0  1 -1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector  0  1  1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector  1 -1 -1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector  1 -1  0)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector  1 -1  1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector  1  0 -1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector  1  0  1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector  1  1 -1)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector  1  1  0)) (build-sponge (- n 1) o) (pop)
            (push) (translate (vector  1  1  1)) (build-sponge (- n 1) o) (pop)
        )
    )
    (pop)
)

(clear-lights)
(clear)

(define L1 (make-light 0))
(light-position L1 (vector 0 0 0))
(light-ambient L1 (vector 0 0 0.1))
(light-specular L1 (vector 0 4 0))
(light-diffuse L1 (vector 1.5 0 0))

(shinyness 10)
(colour (vector 0.75 0.75 1))
(ambient (vector 0.2 0.1 0.1))
(specular (vector 0.1 0.2 0.1))
(emissive (vector 0 0 0))
(opacity 1)
(scale (vector 8 8 8))

(build-sponge 3 build-cube)

I couldn't go any higher than (build-sponge 4 build-cube) without running out of memory.

After that, I made a randomized tree thing, with the general idea that the cross-sectional area of the forked branches totals the area of the trunk branch at each division:

(save-name "rtree.scm")

(define (build-rleaf)
    (push)
    (translate (vector 0 0.5 0))
    (scale (vector 0.5 1 0.5))
    (colour (vector 0 1 0))
    (build-sphere 4 4)
    (pop)
)

(define (build-rtree area)
    (push)
    (rotate (vector 0 65 0))
    (translate (vector 0 0.7 0))
    (scale (vector 0.8 (+ 0.8 area) 0.8))
    (push)
      (scale (vector (sqrt area) (+ 0.8 area) (sqrt area)))
      (colour (vector 0.4 0.3 0))
      (build-sphere 4 4)
    (pop)
    (if (< area 0.001)
        (build-rleaf)
        (begin (let ((split (+ (/ (flxrnd) 1.5) 0.1665)))
            (let ((a1 (* split area)) (a2 (* (- 1 split) area)))
                (rotate (vector 0 0 -20))
                (build-rtree a1)
                (rotate (vector 0 0 55))
                (build-rtree a2)
            )
        ))
    )
    (pop)
)

(clear)
(scale (vector 3 3 3))
(translate (vector 0 -2 0))
(rotate (vector 0 -45 0))
(build-stree 0.2)

And I also had some fun with the turtle builder, making Koch curves:

(define (koch n a)
    (turtle-prim 0)
    (turtle-reset)
    (koch-loop n 6 a (/ 180 a))
    (turtle-vert)
    (turtle-build)
)

(define (koch-loop n s a d)
    (if (> n 0)
        (begin
            (koch-loop (- n 1) (/ s d) a d)
            (turtle-turn (vector 0 0 a))
            (koch-loop (- n 1) (/ s d) a d)
            (turtle-turn (vector 0 0 (* -2 a)))
            (koch-loop (- n 1) (/ s d) a d)
            (turtle-turn (vector 0 0 a))
            (koch-loop (- n 1) (/ s d) a d)
        )
        (begin
            (turtle-vert)
            (turtle-move s)
        )
    )
)

(define (kochs n a)
    (translate (vector 0 3 0))
    (koch n a)
    (if (> n 0)
        (kochs (- n 1) a)
    )
)

(define (kochss n as)
    (if (< 0 (length as))
        (begin
            (push)
            (kochs n (car as))
            (pop)
            (translate (vector 7 0 0))
            (push)
            (kochss n (cdr as))
            (pop)
        )
    )
)

(clear-colour (vector 1 1 1))
(clear)

(hint-unlit)
(hint-wire)
(line-width 1)

(scale (vector 0.5 0.5 1))
(translate (vector -17 -12 0))
(colour (vector 1 0 0))
(kochss 6 (list 60 72 75 80 90))