mathr / blog / #

Starting from this post I'll be using MathJax to display prettier equations. It does require Javascript, but it's much less awkward than the alternatives I've considered.

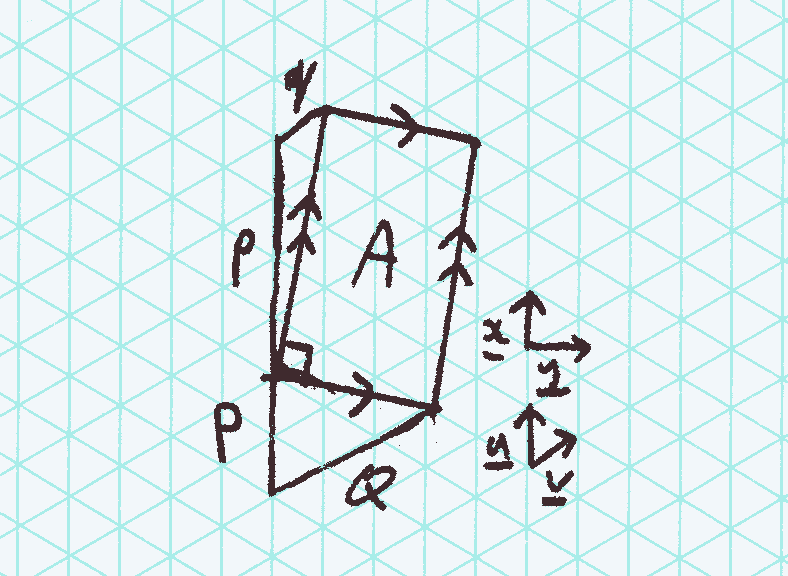
I was wondering about drawing rectangles on a regular triangular lattice. I found that the area is always a multiple of 4 cells.

Let $\mathbf{u},\mathbf{v}$ be the basis vectors of the triangular lattice, and $\mathbf{x},\mathbf{y}$ be the basis vectors of rectangular Cartesian coordinates. Specify a point on the lattice by $p,q \in \mathbb{Z}$, then:

$$p \mathbf{u} + q \mathbf{v} = (p + \frac{q}{2}) \mathbf{x} + \frac{\sqrt{3}}{2} q \mathbf{y}$$

with the squared Euclidean distance of the point from the origin being:

$$\left|\left| p \mathbf{u} + q \mathbf{v} \right|\right| ^ 2= p^2 + q^2 + pq$$

Now assume $\gcd(p,q) = 1$, to ensure that the line segment from the origin to the point passes through no other lattice points. A line $(P,Q)$ perpendicular to $(p,q)$ satisfies:

$$(p + \frac{q}{2}) \mathbf{x} + \frac{\sqrt{3}}{2} q \mathbf{y} = \lambda ( -\frac{\sqrt{3}}{2} Q \mathbf{x} + (P + \frac{Q}{2}) \mathbf{y} )$$

which reduces to

$$\frac{P}{Q} = - \frac{p + 2 q}{2 p + q}$$

Letting $K = \gcd(p + 2 q, 2 p + q)$, then $P = -\frac{p + 2 q}{K}$ and $Q = \frac{2 p + q}{K}$ and $\gcd(P,Q) = 1$.

The area of the rectangle can be found in terms of $p$ and $q$:

$$A^2 = (p^2 + q^2 + pq) (P^2 + Q^2 + PQ)$$

which reduces to

$$A = \sqrt{3} \frac{p^2 + q^2 + pq}{K}$$

Expressing this in terms of the smallest triangular cell on the lattice, which has area $\frac{\sqrt{3}}{4}$, gives a count of triangles:

$$N = 4 \frac{p^2 + q^2 + pq}{K}$$

Recall that $\gcd(p,q) = 1$ and $\gcd(p + 2 q, 2 p + q) = K$. This means that $K \mid p + 2 q$ and $K \mid 2 p + q$ which implies that $K \mid 3 (p + q)$. So $K \mid 3$ or $K \mid p + q$. When $K$ doesn't divide $p + q$ then $K \in \{1,3\}$. Suppose $K \mid p + q$, then $K \mid p + 2 q$ implies that $K \mid q$, and similarly $K \mid 2 p + q$ implies that $K \mid p$. But $\gcd(p,q) = 1$, therefore $K = 1$.

$K = 1$ implies that $4 \mid N$, so it remains to consider the other case when $K = 3$. Let $p = 3 a + b$ and $q = 3 c + d$ with $b,d \in \{0,1,2\}$. Now $K \mid b + 2 d$ and $K \mid 2 b + d$. Exhaustive case analysis shows that this holds only when $b = d$. Expanding

$$p^2 + q^2 + pq = 3(\ldots) + b^2 + d^2 + bd = 3(\ldots) + 3 b^2$$

shows that $3 \mid p^2 + q^2 + pq$. So $\frac{p^2 + q^2 + pq}{K}\ \in \mathbb{Z}$ and $4 \mid N$: the area of a rectangle on a triangular lattice is always a multiple of 4 cells.