mathr / blog / #

Back in August 2011 I was playing around with gnuplot trying to draw curves with constant perpendicular width. I came up with an approximation valid for relatively narrow widths (compared to the curvature):

\[ g_\pm = f \pm K \sqrt{ 1 + \left( \frac{\mathrm{d}f}{\mathrm{d}x}\right)^2 } \]

At the time I didn't explain how it worked. This diagram shows the derivation process:

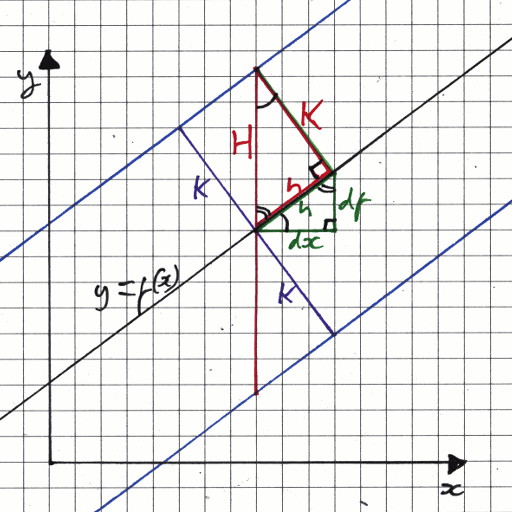
The slope of the curve \(f\) at a point is given by \(\frac{\mathrm{d}f}{\mathrm{d}x}\). Pretending it isn't a limit of infinitesimals for the moment, construct a right-angled triangle under the curve with sides \(\mathrm{d}x\) and \(\mathrm{d}f\). Then its hypotenuse can be calculated by Pythagoras Theorem: \(h = \sqrt{{\mathrm{d}x}^2 + {\mathrm{d}f}^2}\). Now construct a similar triangle along \(h\), whose hypotenuse \(H\) is what we are trying to find. The similarity between triangles gives:

\[ \frac{H}{K} = \frac{h}{\mathrm{d}x} = \frac{\sqrt{ {\mathrm{d}f}^2 + {\mathrm{d}x}^2 }}{\mathrm{d}x} = \sqrt{ 1 + \left( \frac{\mathrm{d}f}{\mathrm{d}x}\right)^2 } \]

which gives the approximation \(g_\pm\) above. The picture at the top shows that it works ok for the most part, but breaks down (see the top right part of the image) when the width is large compared to the radius of curvature.

The picture was generated with an OpenGL fragment shader (using Fragmentarium to do all the boring stuff and let me concentrate on the bit that matters):

#include "2D.frag"

float f(float x) {
  return 0.0625 * sin(6.28 * exp(3.5 - sqrt(abs(2.0 - x))));
}

vec3 color(vec2 c) {
  float x = c.x;
  float y = f(x);
  float y0 = (c.y + 1.0) * 4.0;
  float k = floor(y0);
  y0 -= k + 0.5;
  y0 /= 4.0;
  k = pow(k + 2.0, 1.5) / 1024.0;
  float dy = k * sqrt(1.0 + pow(dFdx(y) / dFdx(x), 2.0));
  float z = floor(abs(y0 - y) / dy);
  return vec3(z);
}

The technique is to compare the function at the x-coordinate of each pixel with the y-coordinate of that pixel - if it's closer than the \(H\) at that x-coordinate then the pixel is inside the fat curve. This shader has a bit more complexity, to draw multiple curves of different widths in one image.

Yesterday I was trying to find a better approximation, but it is impossible to do it perfectly, because even when \(f\) is a function (taking exactly one value for each input), a parallel curve to it might not be (it can even intersect itself). Drawing parametric curves in a fragment shader is a lot harder than drawing functions, but it could be interesting to use the parallel curves to generate vertices for triangle strips.