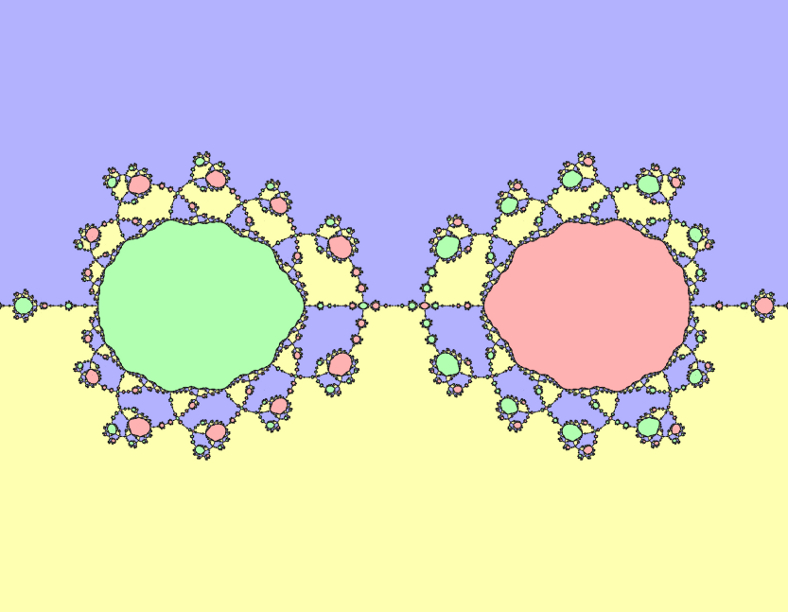
Calendar 2015 - Two Beetles Meet Where Land Meets Sky
Distance estimated Newton fractal for a rational function with zeros at {1, i, -1, -i} and poles at {-2, 2}. I already blogged about this calendar image for March: Distance estimation for Newton fractals. The only other thing to mention is dual numbers for differentiation, which I used to save effort computing derivative equations in an OpenGL GLSL fragment shader re-implementation for Fragmentarium:
#include "Progressive2D.frag"
const int nzeros = 4;
const vec2[4] zeros = vec2[4]
( vec2( 1.0, 0.0)
, vec2( 0.0, 1.0)
, vec2(-1.0, 0.0)
, vec2( 0.0, -1.0)
);
const int npoles = 2;
const vec2[2] poles = vec2[2]
( vec2( 2.0, 0.0)
, vec2(-2.0, 0.0)
);
const vec3[4] colours = vec3[4]
( vec3(1.0, 0.7, 0.7)
, vec3(0.7, 0.7, 1.0)
, vec3(0.7, 1.0, 0.7)
, vec3(1.0, 1.0, 0.7)
);
const float weight = 0.25; // change this according to render size
const float huge = 1.0e6;
const float epsSquared = 1.0e-6;
const int newtonSteps = 64;
float cmag2(vec2 z) { return dot(z,z); }
vec2 csqr(vec2 z) { return vec2(z.x*z.x - z.y*z.y, 2.0*z.x*z.y); }
vec2 crecip(vec2 z) { float d = cmag2(z); return z / vec2(d, -d); }
vec2 cmul(vec2 a, vec2 b) { return vec2(a.x*b.x - a.y*b.y, a.x*b.y + a.y*b.x); }
// dual numbers
vec4 constant(vec2 z) { return vec4(z, 0.0, 0.0); }
vec4 variable(vec2 z) { return vec4(z, length(vec4(dFdx(z), dFdy(z))), 0.0); }
vec4 crecip(vec4 z) { vec2 w = crecip(z.xy); return vec4(w, -cmul(z.zw, csqr(w))); }
vec4 newtonStep(vec4 z) {
vec4 s = vec4(0.0);
for (int i = 0; i < nzeros; ++i) {
s += crecip(z - constant(zeros[i]));
}
for (int i = 0; i < npoles; ++i) {
s -= crecip(z - constant(poles[i]));
}
return z - crecip(s);
}
vec3 newton(vec4 z00) {
vec4 z0 = z00;
bool done = false;
int count = -1;
vec3 rgb = vec3(0.0);
float d0 = huge;
float d1 = huge;
for (int n = 0; n < newtonSteps; ++n) {
d1 = d0;
z0 = newtonStep(z0);
d0 = huge;
for (int i = 0; i < nzeros; ++i) {
float d = cmag2(z0.xy - zeros[i]);
if (d < d0) { d0 = d; rgb = colours[i]; }
}
if (d0 < epsSquared) {
done = true;
break;
}
}
float de = 0.0;
if (done) {
de = 0.5 * abs(log(d0)) * sqrt(d0) / length(z0.zw);
}
return tanh(clamp(weight * de, 0.0, 8.0)) * rgb;
}
vec3 color(vec2 z) { return newton(variable(z * 1.5)); }You can download the above "Two Beetles Meet" Fragmentarium reimplementation.