Coupled oscillator crisis
Simple harmonic motion is the solution to the differential equation:
\[\frac{\partial^2}{\partial t^2} x = -\omega^2 x\]
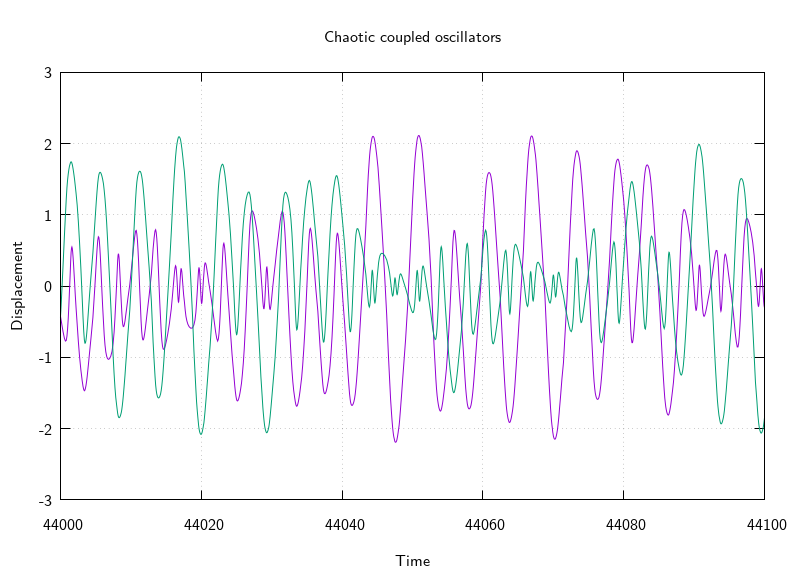
Interested in chaos I wanted to make the angular frequency \(\omega\) be cross-coupled in a pair of oscillators, and I came up with this differential equation:
\[\begin{aligned} \frac{\partial^2}{\partial t^2} x &= -e^{y^2} x \\ \frac{\partial^2}{\partial t^2} y &= -e^{x^2} y \end{aligned}\]
It sounds something like this: audio snippet.
I initially experimented with Octave's ode45() function, but it was rather slow, so I ported it to C99 (specialized to 4-vectors containing the displacement and velocity of each oscillator). Unfortunately it exploded after some time, with the amplitude of the oscillators swinging ever-larger, and the frequency of oscillation getting very very high too (which meant that the adaptive step size Runge-Kutta integration scheme would effectively get stuck and stop making progress).
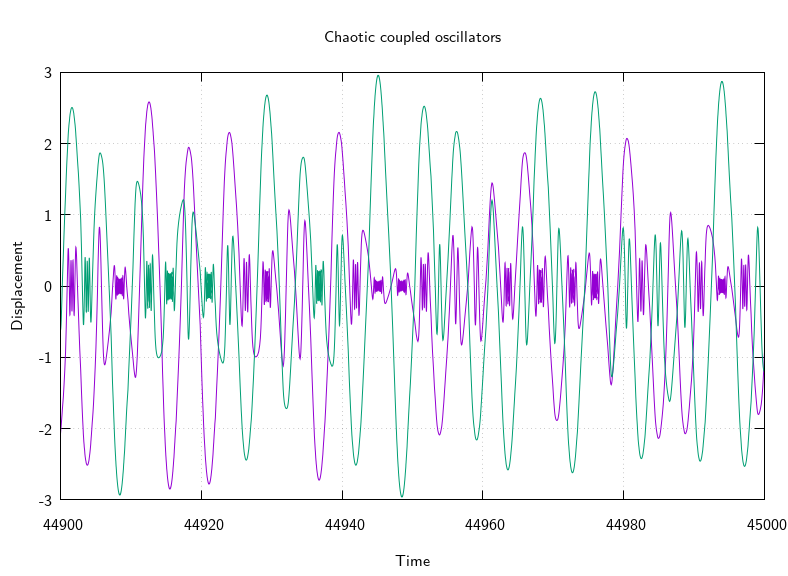
Investigating this crisis, I thought to plot the energy of the system, and sure enough it exploded:
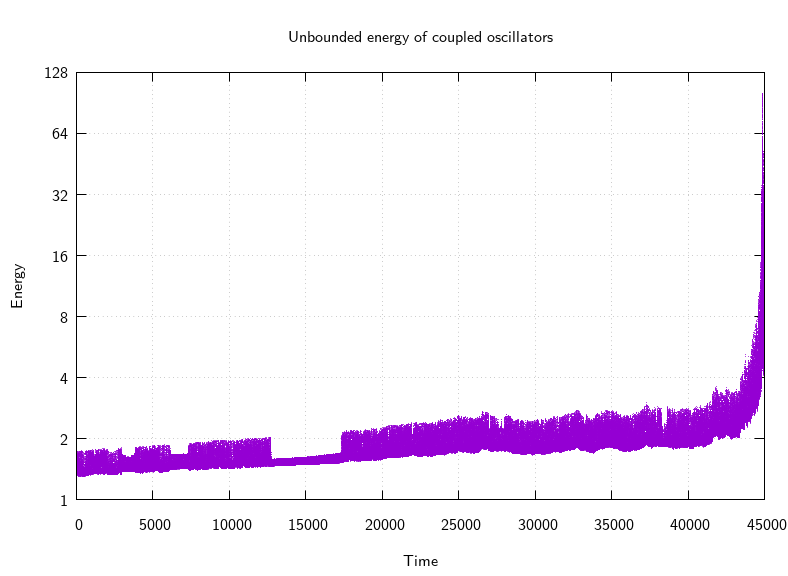
So this experiment failed, I'll have to try some other coupling expressions to see if they suffer the same fate or otherwise. Eventually I wanted to try controlling chaos by small perturbations to nudge the oscillators into unstable periodic orbits of various kinds, but no joy this week.
You can download the C source code for the integration calculations, gnuplot source code for the diagrams, and Octave source code for converting to audio.