mathr / blog / #

It is known that in the Mandelbrot set, the smallest hyperbolic component of a given period is in the utter west of the antenna. Each atom is 16 times smaller and 4 times nearer the tip, which also means each successive atom domains is 4 times smaller (they all meet at the tip). This gives atom size \(O(16^{-p})\) and domain size \(O(4^{-p})\) where \(p\) is the period. I verified this relationship with some code:

#include <stdio.h>
#include <mandelbrot-numerics.h>

int main()
{
  for (int period = 1; period < 64; period += 1)
  {
    printf("# period %d\n", period);
    fflush(stdout);
    mpfr_prec_t prec = 16 * period + 8;
    mpc_t guess, nucleus, size;
    mpc_init2(guess, prec);
    mpc_init2(nucleus, prec);
    mpc_init2(size, prec);
    mpc_set_d(guess, -2, MPC_RNDNN);
    while (prec > 2)
    {
      mpfr_prec_round(mpc_realref(guess), prec, MPFR_RNDN);
      mpfr_prec_round(mpc_imagref(guess), prec, MPFR_RNDN);
      m_r_nucleus(nucleus, guess, period, 64);
      printf("%ld ", prec);
      fflush(stdout);
      m_r_size(size, nucleus, period);
      mpc_norm(mpc_realref(size), size, MPFR_RNDN);
      mpfr_log2(mpc_realref(size), mpc_realref(size), MPFR_RNDN);
      mpfr_div_2ui(mpc_realref(size), mpc_realref(size), 1, MPFR_RNDN);
      mpfr_printf("%Re ", mpc_realref(size));
      fflush(stdout);
      m_r_domain_size(mpc_realref(size), nucleus, period);
      mpfr_prec_round(mpc_realref(size), 53, MPFR_RNDN);
      mpfr_log2(mpc_realref(size), mpc_realref(size), MPFR_RNDN);
      mpfr_printf("%Re\n", mpc_realref(size));
      fflush(stdout);
      prec--;
      mpfr_prec_round(mpc_realref(nucleus), prec, MPFR_RNDN);
      mpfr_prec_round(mpc_imagref(nucleus), prec, MPFR_RNDN);
    }
    printf("\n\n");
    fflush(stdout);
  }
  return 0;
}

Plotting the output shows it is so:

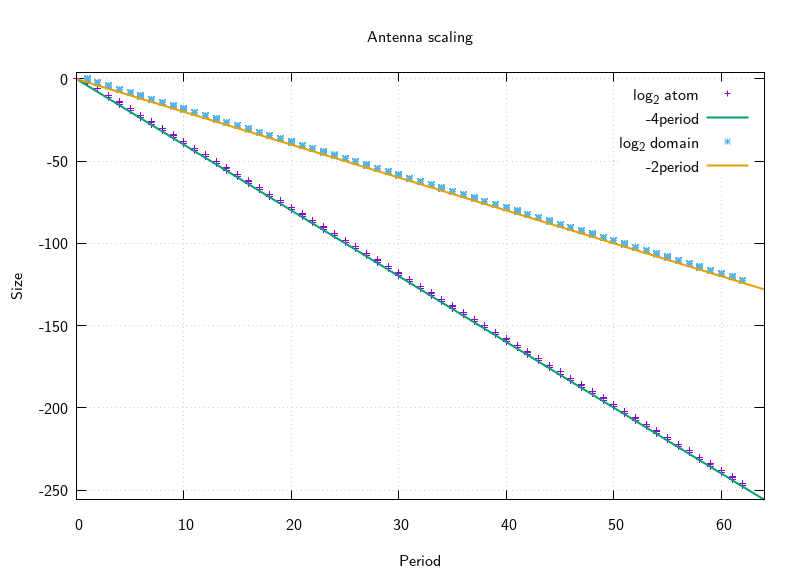
This makes a rough worst case estimate of the precision required to accurately compute a size estimate (whether for atom or domain) from the nucleus of the atom be around \(4 p\) bits. (EDIT 2017-11-08 an earlier version of this post incorrectly stated \(16 p\) bits, but I forgot to take the log2 properly when converting from size to bits required.) But it turns out that (at aleast for this sequence of atoms heading to the tip of the antenna) a lot less precision is actually required. Here's a graph showing a seam where the size estimate breaks down when the precision gets too low, and doing some maths shows that the seam is at precision \(2 p\), a factor of \(2\) better than the first guess:

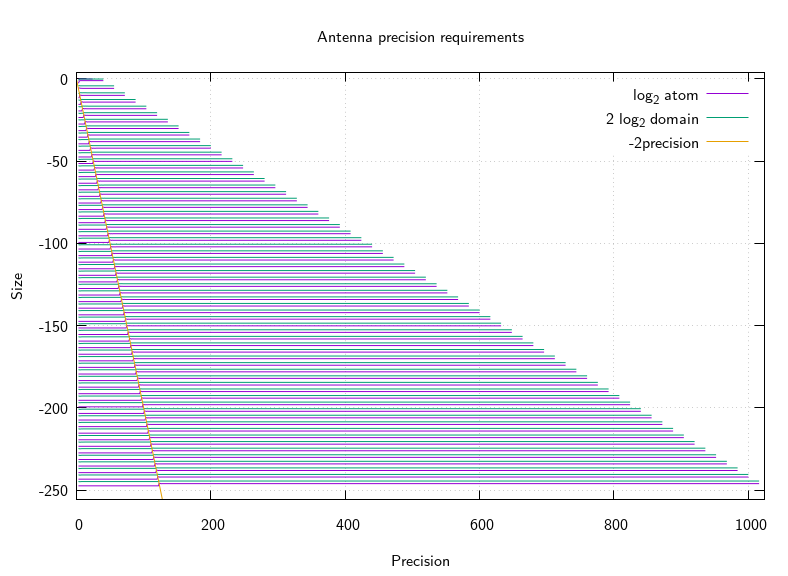
It remains to investigate other sequences of atoms, to see how they behave. Chances are the \(2 p\) bits of precision required estimate is only necessary in rare cases like heading toward filament tips, and that aesthetically-chosen iterated Julia morphing atoms (for example) will be very much larger than would be expected from their period.