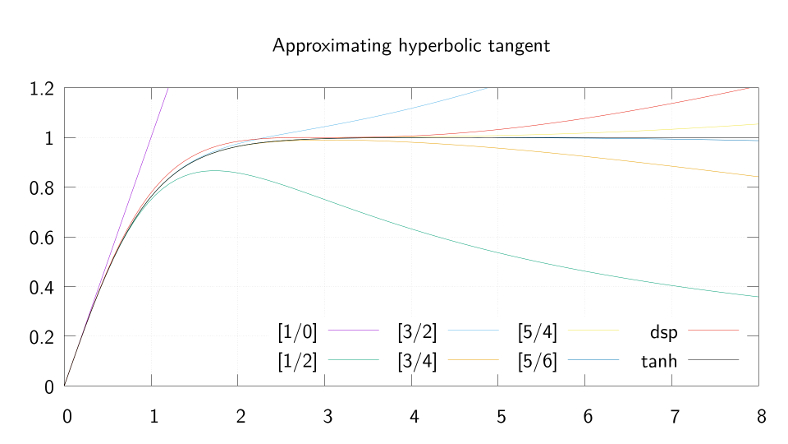
Approximating hyperbolic tangent
tanh() is a nice function for saturation in audio, amongst other applications. Near 0 it is similar to the identity function \(x\), leaving sound unchanged. Far from 0 it tends to constant \(\pm 1\), with a smooth roll-off curve that gives a soft-clipping effect, where louder signals are more distorted, and the output never exceeds 0dBFS.
Unfortunately tanh() is computationally expensive, so approximations are desirable. One common approximation is a rational function:
\[ \tanh(x) \approx x \frac{27 + x^2}{27 + 9 x^2} \]
which the apparent source describes as
based on the pade-approximation of the tanh function with tweaked coefficients.
I also found mention Padé-approximants on a page primarily focussed on approximating tanh() with a continued fraction. So I set out to discover what they were. Some dead ends (a book appendix with 6 pages of badly-OCR'd FORTRAN code, to name but one) and I eventually struck gold with this PDF preview:
Outlines of Padé Approximation by Claude Brezinski in Computational Aspects of Complex Analysis pp 1-50 part of the NATO Advanced Study Institutes Series book series (ASIC, volume 102)
Abstract: In the first section Padé approximants are defined and some properties are given. The second section deals with their algebraic properties and, in particular, with their connection to orthogonal polynomials and quadrature methods. Recursive schemes for computing sequences of Padé approximants are derived. The third section is devoted to some results concerning the convergence problem. Some applications and extensions are given in the last section.
The preview contains a system of equations involving a rational function:
\[ [p/q]_f := \frac{\sum_{i=0}^p a_i x^i}{\sum_{i=0}^q b_i x^i} \]
where without loss of generality \(b_0 = 1\). The coefficients are derived from the coefficients \(c_i\) of the Maclaurin series of \(f\) (which is its Taylor series expanded about \(0\)):
\[ f := \sum_{i=0}^\infty c_i x^i \]
The system of equations is very regular, here's some Haskell code to solve for the \(a\)s and \(b\)s given the \(c\)s:
pade :: [Rational] -> Int -> Int -> ([Rational], [Rational])
pade c p q = (a, b)
where
m = take q . map (take q) . tails . drop (p - q + 1) $ c
v = take q . drop (p + 1) . map negate $ c
Just m1 = inverse m -- FIXME this will crash if it isn't invertible
b = 1 : reverse (m1 `mulmv` v)
a = take (p + 1)
$ [ reverse cs `dot` bs
| (bs, cs) <- map unzip . drop 1 . inits $ zip (b ++ repeat 0) c
]This needs an inverse :: [[Rational]] -> Maybe [[Rational]], the
pure Gaussian elimination code from
an old mailing list post
works fine with minor modifications for current GHC versions (it needs an extra
Eq constraint now).
With some extra output beautification code (and of course the coefficients of the power series for tanh(), which involve the Bernoulli numbers) the first few Padé approximants for tanh() are:
[1/0] = x [1/2] = x*(3)/(3+x**2) [3/2] = x*(15+x**2)/(15+6*x**2) [3/4] = x*(105+10*x**2)/(105+45*x**2+x**4) [5/4] = x*(945+105*x**2+x**4)/(945+420*x**2+15*x**4) [5/6] = x*(10395+1260*x**2+21*x**4)/(10395+4725*x**2+210*x**4+x**6) [7/6] = x*(135135+17325*x**2+378*x**4+x**6)/(135135+62370*x**2+3150*x**4+28*x**6) [7/8] = x*(2027025+270270*x**2+6930*x**4+36*x**6)/(2027025+945945*x**2+51975*x**4+630*x**6+x**8)
Some of these are shown in the image at the top of this post, along with the music-dsp approximation with "tweaked coefficients". The [7/6] approximation agrees with the truncated Lambert's continued fraction from the linked page, I'll probably end up using the [5/6] in various experiments. You can download the source code here: Pade.hs.