Trustworthy fractals
Last week I implemented (in Haskell, using lazy ST with each STRef paired with Natural so that I can have Ord) the algorithm presented in this paper:
Images of Julia sets that you can trust
L. H. de Figueiredo, D. Nehab, J. Stolfi, and J. B. Oliveira
Last updated on January 8, 2013 at 10:45am.
Abstract: We present an algorithm for computing images of quadratic Julia sets that can be trusted in the sense that they contain numerical guarantees against sampling artifacts and rounding errors in floating-point arithmetic. We use cell mapping and color propagation in graphs to avoid function iteration and rounding errors. As a result, our algorithm avoids point sampling and can robustly classify entire rectangles in the complex plane as being on either side of the Julia set. The union of the regions that cannot be so classified is guaranteed to contain the Julia set. Our algorithm computes a refinable quadtree decomposition of the complex plane adapted to the Julia set which can be used for rendering and for approximating geometric properties such as the area of the filled Julia set and the fractal dimension of the Julia set.
Keywords: Fractals, Julia sets, adaptive refinement, cellular models, cell mapping, computer-assisted proofs
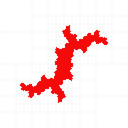
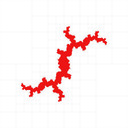
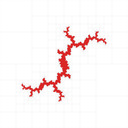
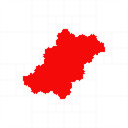
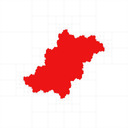
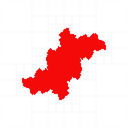
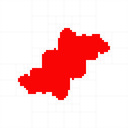
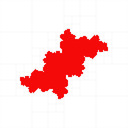
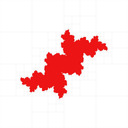
You can find my code in my mandelbrot-graphics repository. I reproduced most of the results, I coloured with black interior, white exterior, red unknown (Julia set is inside the red region), and the quad tree cell boundaries in grey:
The last two examples above show how it fails at parabolic Julia sets.
I also implemented a trustworthy Mandelbrot set, based on the idea that if the neighbourhood of the origin in the Julia is all exterior, then the point cannot be in the Mandelbrot set, and if any interior exists in the Julia set, then the point must be in the Mandelbrot set. Now replace 'point' in those two clauses with "closed 2D square", and use the property of the algorithm in the paper that means the proofs for interiorhood and exteriorhood of the Julia set range over the interval.
It's far too slow to be practical, if pretty pictures were the goal! The red zone of unknown doesn't shrink much with each depth increment.