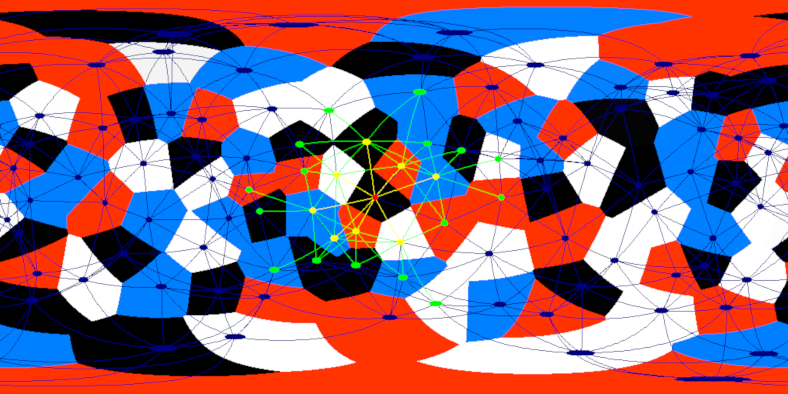
meshwalk-3.0
meshwalk-3.0 is a 360 animation of animated Voronoi cells on the surface of a sphere. Rapid acceleration is highlighted visually and sonified spatially. The movement of the dynamic mesh in this version is partly based on the idea of potential wells for crystal formation, and is realized efficiently by updating a collection of nearest neighbours to each node using the neighbours of neighbours (and hoping that it doesn't move so fast that the algorithm would break).
At each time step, after updating the positions of each node (which depends on attraction and repulsion between neighbouring cells), the neighbour list of each cell is updating by choosing the 8 nearest cells among the neighbours and neighbours of neighbours. As the nodes are moving, a neighbour of neighbour might now be nearer than the previous neighbours, so the mesh is dynamically changing. The number 8 can be changed at compile time, too high and it slows down, too low and it breaks (the mesh splits apart and can overlap itself without rejoining).
This mesh algorithm is O(N B^2), where N is the number of nodes and B is the number of neighbours to keep track of. As B is typically a small constant, this reduces to O(N). A naive algorithm is O(N^2) considering all nodes for each node, which I do do in the one-time initialization of the neighbour data. A spatial data structure could probably reduce this cost to O(N log N), but for a few hundred nodes on a sphere it isn't too slow. The Vornoi cell rendering is O(N W H), my GPU is fast so it isn't an issue.