mathr / blog / #

So I was playing around with FAuSt, a pure functional dataflow language for audio stream processing. At first I thought it was great, but then the compiler bugs bit hard: declaring two variables with the same name in the same scope made the compiler segfault [2010-01-13 update: I have not been able to reproduce this crash, so I'm probably wrong about the cause], and for some reason it thought the index variables in my parallel constructs were duplicates too. I was trying to build a 16x16 matrix multiplication to implement my favourite reverb... perhaps too ambitious? Simple things are very concise in FAuSt, though: I implemented Pure-data's vcf~ in roughly the same number of characters as the number of lines of code that the C implementation had:

vcf(q,f,x) = w ~ (_,_) with {
  a = max(f * 2 * PI / SR, 0);
  r = max(1 - a / q, 0);
  c = r * cos(a);
  s = r * sin(a);
  k = (2 - 2 / (q + 2)) * (1 - r);
  w(u,v) = (k * x + c * u - s * v) , (s * u + c * v);
};

So I thought to myself, with Haskell's awesomeness I should be able to embed the core of the FAuSt block diagram algebra semantics in a typesafe way. Much headsploding followed, figuring out how to bluff my way through type-level programming, until I managed to express the preconditions and results of each of the five block diagram composition operators.

It might help to know what a block diagram is and how they can be composed. For that I recommend Chapter 3 of A FAuSt Tutorial (PDF). I decided that GADTs were what I needed, with constructors for each of the composition operators, and one for primitives:

-- abstract block diagrams
data Bd t where
  Rec   :: (...) => Bd i -> Bd j -> Bd k
  Par   :: (...) => Bd i -> Bd j -> Bd k
  Seq   :: (...) => Bd i -> Bd j -> Bd k
  Split :: (...) => Bd i -> Bd j -> Bd k
  Merge :: (...) => Bd i -> Bd j -> Bd k
  Prim  :: (...) => String  -> k -> Bd k

I've omitted the contexts here, because they are quite long, expressing the necessary preconditions on the shapes of the block diagram inputs and the resulting output block diagram shape. I'm using "shape" to mean a pair of type-level lists, for example a standard (+) :: Float -> Float -> Float operator lifted to a block diagram could have a shape like (Float :. Float :. Nil, Float :. Nil), depending on how spicy you like your curry.

FAuSt semantics for the recursive composition operator A~B are described informally like this (where (i|o)X is the number of inputs|outputs of X):

• the first iB outputs of A are fed into the inputs of B
• the outputs of B are fed into the first oB inputs of A
• the remaining iA-oB inputs of A are the inputs of A~B
• the oA outputs of A are the outputs of A~B

From this description it's easy to see the requirement that oA>=iB and iA>=oB, moreover the types of the inputs must match the types of the outputs they are connected to. This precondition on the compatibility of the shapes, and the shape of their composition, can be expressed like this:

-- recursive composition compatibility and result shape
type family IsRecCompat x y
type instance IsRecCompat (xi, xo) (yi, yo) = (Take (Length yi) xo `Equals` yi) :&&: (Take (Length yo) xi `Equals` yo)
type family RecShape x y
type instance RecShape (xi, xo) (yi, yo) = (Drop (Length yo) xi, xo)

Here Take, Drop, Length, and Equals operate on type-level lists. The full type of the Rec constructor is now:

  -- recursive composition constructor
  Rec   :: (NaturalT (Length ai), NaturalT (Length ao),
            NaturalT (Length bi), NaturalT (Length bo),
            NaturalT (Length ci), NaturalT (Length co),
            i ~ (ai,ao), j ~ (bi,bo), k ~ (ci,co),
            IsRecCompat   i j ~ True, RecShape   i j ~ k)
        => Bd i -> Bd j -> Bd k

where the first 4 lines express that the lengths of the lists are non-negative numbers and that the shapes are pairs of lists - not sure how to simplify this boilerplate which is present for all the operators, but it seems to work ok.

With the fixities as in FAuSt...

infixl 4 `Rec`
infixl 3 `Par`
infixl 2 `Seq`
infixl 1 `Split`
infixl 1 `Merge`

...and suitable definitions of primitives, it's possible to write expressions that look like a more verbose FAuSt, and manipulate them in various ways:

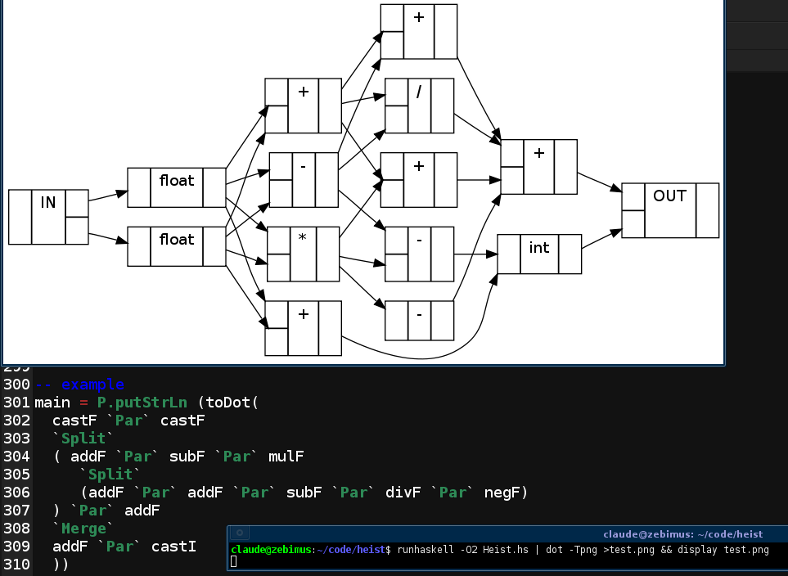
-- example
main = putStrLn (toDot(
  castF `Par` castF
  `Split`
  ( addF `Par` subF `Par` mulF
     `Split`
     (addF `Par` addF `Par` subF `Par` divF `Par` negF)
  ) `Par` addF
  `Merge`
  addF `Par` castI
  ))

I won't talk about the toDot code right now, as it's not too impressive compared to the rest of the code - but if you want to look the whole lot is in my messy Subversion repository:

svn co https://code.goto10.org/svn/maximus/2009/heist heist

And why the name Heist? Maybe I'm trying to steal FAuSt's thunder! Or it could just be that it's got an H and an S in it...