Heist: busted!

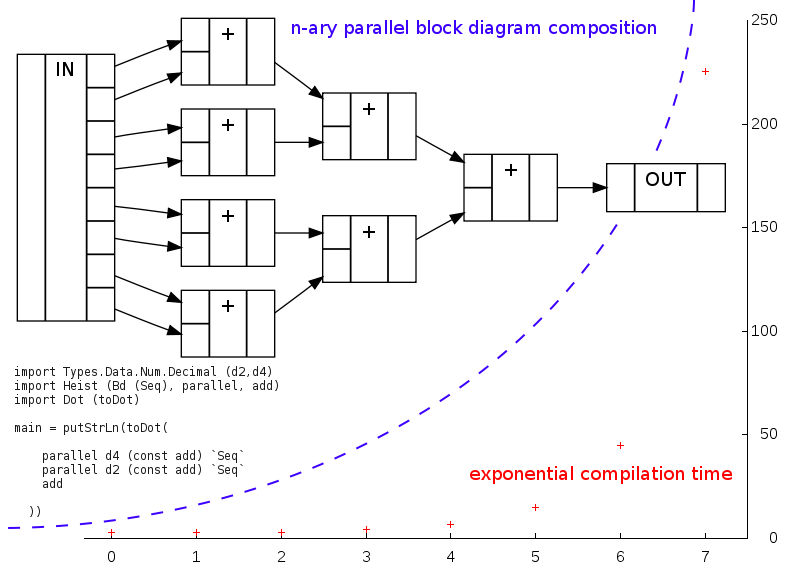
FAuSt has a nifty n-ary block diagram parallel composition operator, in which you give it a count and a function from numbers to block diagrams. Something with the same meaning as:

parallel n f = foldr1 Par (map f [0..(n-1)])

If only life were so simple: that won't compile, because of my decision in Heist to express the type system of block diagram algebra within Haskell's type system. So after about 4 hours of head scratching, I finally figured out how to generalize from this:

par0 f = empty
par1 f = par0 f `Par` f 0
par2 f = par1 f `Par` f 1
par3 f = par2 f `Par` f 2
par4 f = par3 f `Par` f 3
...

to the point where this compiles successfully:

import Types.Data.Num.Decimal (d2, d4)
import Heist (Bd (Seq), parallel, add)
import Dot (toDot)

main = putStrLn(toDot(

    parallel d4 (const add) `Seq`
    parallel d2 (const add) `Seq`
    add

  ))

Check out the code to see the horrible gory details, where at the time of writing (Subversion revision 1582) the relevant excerpt is lines 222-256 of Heist.hs:

svn co https://code.goto10.org/svn/maximus/2009/heist heist

At this point I was happy and delighted, but not for long. I tried to compile a program containing parallel d8 add and waited, and waited, only to find (7.5 minutes later...) that GHC reached my operating system's limit of 3GB per process and gave up. It was a similar story when explicitly limiting the heap size. I ran some tests and it seemed that the compilation time grew exponentially with the parallel count.

The "shortcut" of embedding FAuSt semantics inside Haskell to avoid having to write a parser and type checker and all the rest turned out to be a rather more "scenic route" through type level programming, but in summary: theoretically beautiful, epic fail in practice.