Dithering
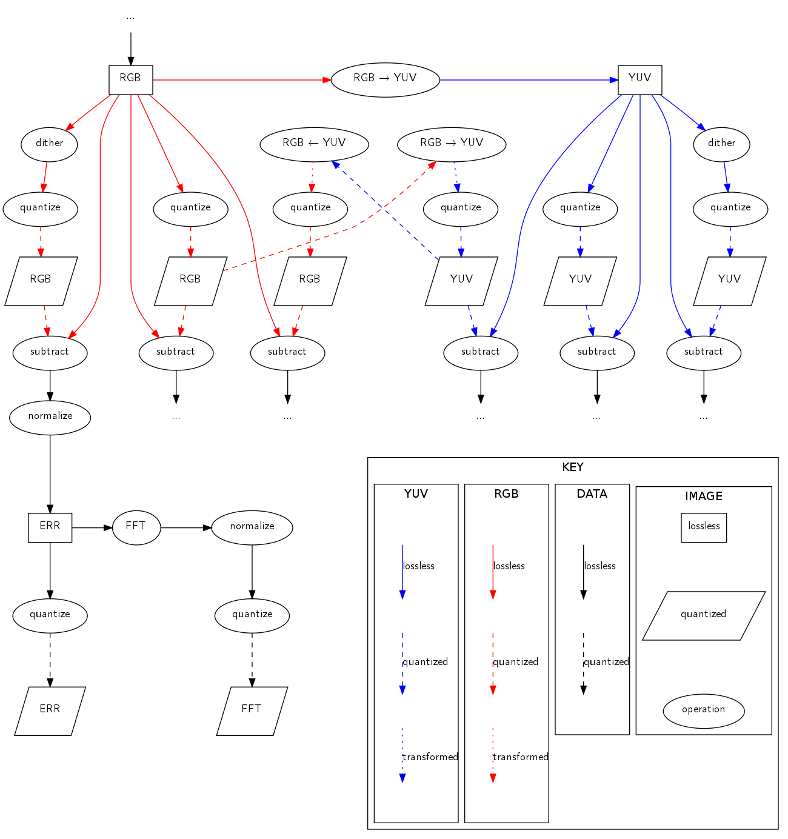
Some image formats (like PNG) use RGB, some (like JPEG) use YUV which separates out the colour information from the brightness information (originating in the early history of colour television). Colour space transformation is theoretically lossless, but most image formats store data as small integers (usually 8bit, which gives 256 shades for each colour channel). If you save an RGB image (already quantized) to JPEG, it'll be converted to YUV and quantized again. Then when you load it, it'll be converted to RGB and quantized a third time. (The loss from quantization is different from the loss from JPEG compression, which I'm ignoring in this post.)
Quantization (converting from a high precision to a lower precision) requires irreversibly discarding information. Dithering adds a small amount of noise to each channel of each pixel before quantization takes place, which averages out quantization errors across the image. The point I want to make in this post is that dithering improves image quality, at least when starting with lossless computer-generated source material.
A small example: suppose you have a 1bit image format with one channel, each pixel can be 0 (black) or 1 (white). Moreover you have a source image at high precision with a smooth gradient from 0 to 1. When the gradient is at 0.25, quantization gives 0 100% of the time, and when the gradient is at 0.75, quantization gives 1 100% of the time. This gives a sharp transition from black to white at mid-level grey. If you add dither, however, 0.25 will turn out 1 25% of the time and 0 75% of time, and 0.75 will turn out 1 75% of the time and 0 25% of the time. Instead of a sharp transition band, there will be white speckles on a black background that gradually increase in density from no speckles at 0.00 to all speckles at 1.00. Here's an example in 1bit RGB colour:
| dithered | undithered |
|---|---|
 |
 |
In 8bit colour the problem is less visible:
| dithered | undithered |
|---|---|
 |
 |
They look almost identical, but if you bump up the gain you can see the differences more clearly:
| dithered gain boosted | undithered gain boosted |
|---|---|
 |
 |
Comparing with the lossless (well, double-precision floating point) source image, the errors from quantization have a rather different character:
| dithered error | undithered error |
|---|---|
 |
 |
Performing a 2D FFT reveals the spectrum of the error is nearly flat when dithering, but rather dramatic without:
| dithered error FFT | undithered error FFT |
|---|---|
 |
 |
In the worst case (converting RGB to YUV to RGB, quantizing at each stage without dithering), the quantization errors are visible even without bumping up the gain (but I did it anyway):
| undithered via YUV | undithered via YUV gain boosted |
|---|---|
 |
 |
Even with 16bit image formats, the problem isn't eliminated, though it is much less visible - zooming in on the higher-resolution files linked in the table and looking carefully at the dark areas reveals some banding:
| 16bit gain boosted | 16bit via YUV gain boosted |
|---|---|
 |
 |
And if your image viewer doesn't dither when quantizing 16bit images to your (typically 8bit) display depth, you'll get banding as if you hadn't dithered and saved at 8bit anyway. However, the loss from quantizing 3 times during RGB to YUV to RGB is much lower at 16bit, this is the difference between the two last 8bit images amplified 64 times:
| | 16bit gain boosted - 16bit via YUV gain boosted | |
|---|
 |
Final thoughts:
- Dither before quantizing.
- If your target codec uses YUV, convert your high-precision source to high-precision YUV, then see (1).
Source code for this post:
- dither.dot
- graphviz source for the diagram
- dither.c
- C99 source for the image generation program
- dither.csv
- CSV error statistics output from the program