mathr / blog / #

Aaron Klebanoff's 2001 paper \(\pi\) in the Mandelbrot Set got me thinking, in particular the problem in the conclusion:

Another open problem is to determine the function of \(\epsilon\) that multiplies \(N(\epsilon)\). So far, we have \[a \epsilon^b N(\epsilon) \to \pi \] where we have seen \(a = 1, 2\) and \(b = 1, \frac{1}{2}\). In general, should we expect [this limit] to hold for some rational values \(a\) and \(b\)? If so, what does the pinch location in \(M\) tell us about \(a\) and \(b\)?

Here \(\epsilon\) is the distance from a point along a path heading to a cusp or pinch point between two hyperbolic components in the complement of the Mandelbrot set \(M\), and \(N(\epsilon)\) is the iteration count at that point. My conclusion after some scribbling is that \(b = 1\) for all pinch points, and \(a\) is not in general rational. My workings below aren't as formal as Klebanoff's, but hopefully the idea is sound.

As paths through the complement of \(M\) I take the external ray landing at the desired pinch point. The ray passes between lots of child bulbs on either side, which are increasing in period towards the pinch point. The increase is in increments of the period of the smaller (higher period) bulb at the pinch point. The rays landing at the pinch-point side of the roots of these child bulbs come together quickly heading out towards infinity, as they differ only in the last digits of the repeating part of the binary expansions of the corresponding rational external angles. In fact, where corresponding pairs meet in the same grid cell of the pictures below, the iteration count there is the lower of the two periods.

Next, consider the internal angles of the the child bulbs of the smaller (larger period) bulb at the pinch point. These are in the sequence \(\frac{1}{p}\) where \(p\) is the period of the child bulb divided by the period of the parent bulb. Drawing triangles as \(p \to \infty\) shows that the distance to the bulb from the pinch point is approximately \(\epsilon \approx s \tan \frac{2\pi}{p}\) where \(s\) is the radius of the smaller pinch point bulb. Further, as \(\tan \theta \to \theta \text{ as } \theta \to 0\), the distance reduces to \(\epsilon \approx s \frac{2\pi}{p}\).

Now, combining the previous two paragraphs, call the period of the smaller bulb at the pinch point \(P\). Then \(N(\epsilon)\) is approximately \(P p\). Substituting into the expression for \(\epsilon\), we get \(\epsilon \approx s \frac{2\pi P}{N(\epsilon)}\) which simplifies to:

\[ \pi \approx \frac{\epsilon N(\epsilon)}{2 P s}\]

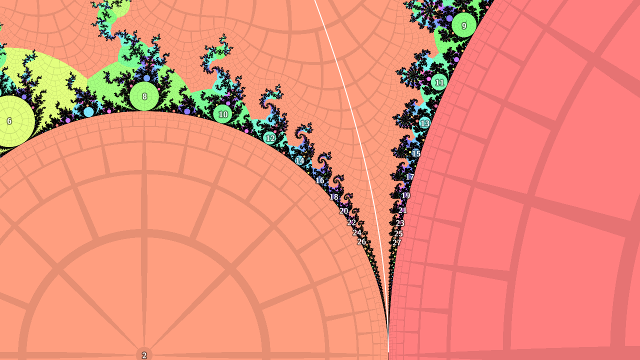
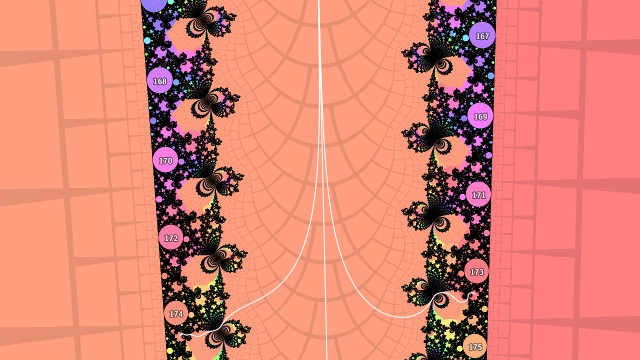
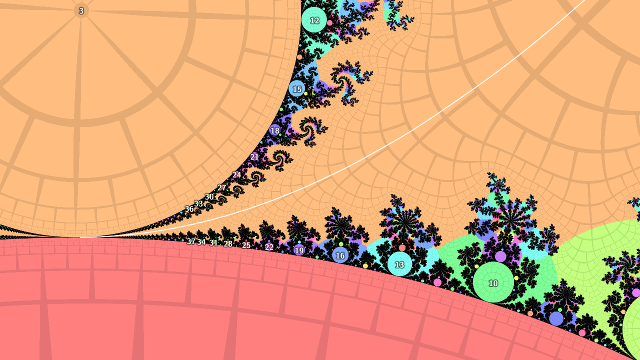
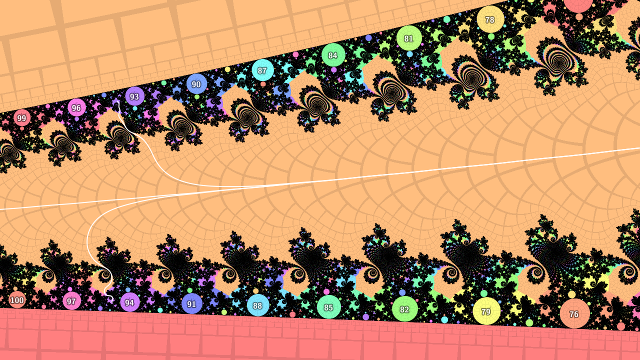
So much for the theory, how does it work out in practice? Not very well, as it turns out. I plotted some numerical results for various external angles, and while they tend to flat lines as the iteration count increases which implies that \(\epsilon N(\epsilon) \to K\) for some constant \(K\), the scaling factors I calculated aren't quite there - the limits are some way off from being \(\pi\).

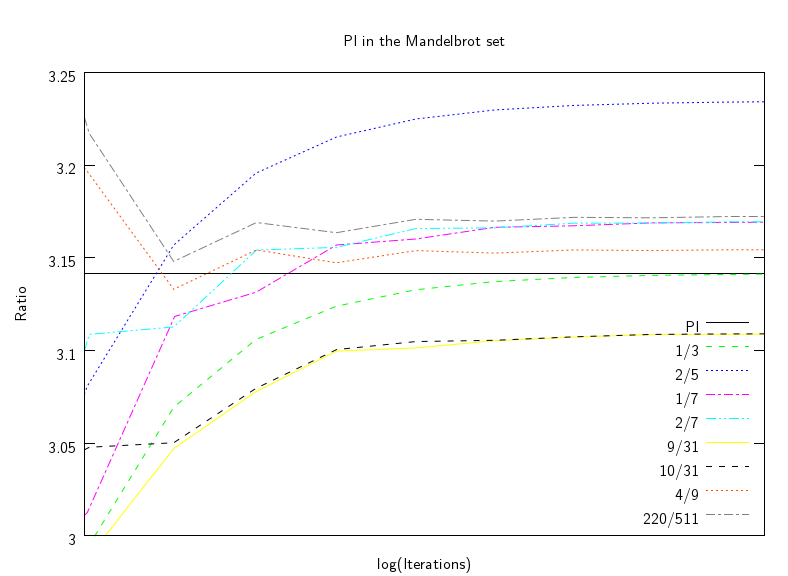
I suspect this is because the internal angles aren't exactly the same as geometric angles (there is a conformal transformation making up the difference), or something else is going wrong, in any case it was a fun experiment to try out - not all experiments give the desired result, which I guess is the point of experimentation in the first place.