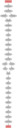mathr / blog / #

Back in 2011 I played around with word edit graphs based on the spelling of words. Recently I've been playing with the same concept applied to the pronunciation of words. I used the Haskell package pronounce to load the CMUDict pronouncing dictionary, but most of my code didn't really use the API of the library - mostly because it uses a reader monad while I wanted to use a random monad for algorithmic poetry generation, which didn't happen yet (but maybe I'll send patches to use a transformer instead of a plain reader).

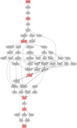
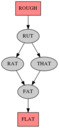
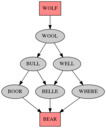
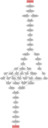
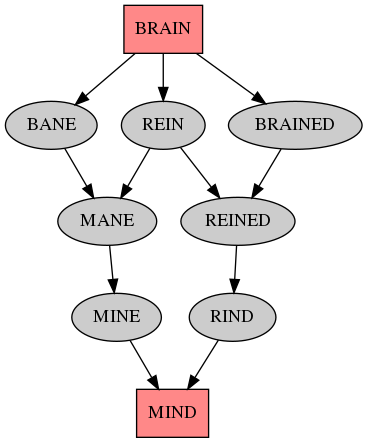
Here's some output:

And here's the code, mostly copy/paste of the 2011 code:

{-# LANGUAGE OverloadedStrings #-}

module Main (main) where

import Prelude hiding (Word)

import Text.Pronounce

import qualified Data.Text as T
import qualified Data.Text.IO as T

import Data.Map (Map)
import qualified Data.Map as M

import Data.Set (Set)
import qualified Data.Set as S

import Control.Monad (forM_, when)
import Data.Char (isDigit, isLower)
import Data.List (inits, tails)
import Data.Maybe (fromMaybe)
import System.Environment (getArgs)


type Dict = (Map Word [Pron], Map Pron [Word])

invert :: (Ord k, Ord v) => Map k [v] -> Map v [k]
invert m = M.fromListWith (++) [(v, [k]) | (k, vs) <- M.toList m, v <- vs]

type Phon = T.Text
type Pron = T.Text
type Word = T.Text

toPron :: Dict -> Word -> [Pron]
toPron (dict, _) word = fromMaybe [] (M.lookup word dict)

fromPron :: Dict -> Pron -> [Word]
fromPron (_, dict) pron = fromMaybe [] (M.lookup pron dict)

editPron :: Pron -> [Pron]
editPron pron = map T.unwords (delete1 s ++ replace1 s ++ insert1 s)
  where s = T.words pron

delete1 :: [Phon] -> [[Phon]]
delete1 [] = []
delete1 (x:xs) = xs : ((x:) <$> delete1 xs)

replace1 :: [Phon] -> [[Phon]]
replace1 [] = [[]]
replace1 (x:xs) =
  [ y:xs
  | y <- {- phonemes -} if x `elem` vowels then vowels else consonants
  ] ++ [ x:ys | ys <- replace1 xs
  ]

insert1 :: [Phon] -> [[Phon]]
insert1 xs =
  [ ys ++ [p] ++ zs
  | (ys, zs) <- zip (inits xs) (tails xs)
  , p <- phonemes
  ]

edit :: Dict -> Word -> [Word]
edit dict word = do
  pron <- toPron dict word
  pron <- editPron pron
  take 1 $ fromPron dict pron

data Graph = Graph
  { nodes :: Set Word
  , edges :: Set (Word, Word)
  , border :: Set Word
  , unused :: Set Word
  }

graph :: Set Word -> Word -> Graph
graph ns s = Graph
  { nodes = S.singleton s
  , edges = S.empty
  , border = S.singleton s
  , unused = S.delete s ns
  }

gGrow :: (Word -> [Word]) -> Bool -> Graph -> Graph -> Maybe (Set (Word, Word))
gGrow f phase source sink
  | (not . S.null) inter = Just . (if phase then gReverse else id) $
      gJoin inter (edges source) (edges sink)
  | S.null sourceNew = Nothing
  | otherwise = gGrow f (not phase) sink source'
  where
    inter = (nodes source `S.intersection` nodes sink)
    neighbours g =
      let (n, e) = unzip . concatMap (step f) . S.toList . border $ g
          ns = unused g `S.intersection` S.fromList n
          es = ((`S.member` unused g) . snd) `S.filter` S.fromList e
      in  (ns, es)
    (sourceNew, sourceEdge) = neighbours source
    source' = source
      { nodes = nodes source `S.union` sourceNew
      , border = sourceNew
      , edges = edges source `S.union` sourceEdge
      , unused = unused source `S.difference` sourceNew
      }

gJoin :: Set Word -> Set (Word, Word) -> Set (Word, Word)
  -> Set (Word, Word)
gJoin inter source sink =
  gPrune inter source `S.union` gReverse (gPrune inter sink)

gPrune :: Set Word -> Set (Word, Word) -> Set (Word, Word)
gPrune ns es
  | S.null ns = S.empty
  | otherwise =
      let keep = S.filter ((`S.member` ns) . snd) es
      in  keep `S.union` gPrune (S.map fst keep) (es `S.difference` keep)

gReverse :: Set (Word, Word) -> Set (Word, Word)
gReverse = S.map swap

swap :: (Word, Word) -> (Word, Word)
swap (x, y) = (y, x)

step :: (Word -> [Word]) -> Word -> [(Word, (Word, Word))]
step f w = (\s -> (s, (w, s))) <$> f w

main :: IO ()
main = do
  args <- map T.pack <$> getArgs
  cmu <- M.map (map (T.filter (not . isDigit))) <$> stdDict
  usr <- readDict
  cmu <- pure $ M.intersection cmu (M.fromList [(w,()) | w <- S.toList usr ])
  dict <- pure $ M.keysSet cmu
  f <- pure $ edit (cmu, invert cmu)
  T.putStrLn $ "digraph G {"
  T.putStrLn $ "node[shape=\"box\",style=\"filled\",fillcolor=\"#ff8888\"];"
          <> T.unwords (map (T.pack . (++";") . show) args)
          <> " node[shape=\"ellipse\",fillcolor=\"#cccccc\"];"
  when (all (`M.member` cmu) args) $
    forM_ (zip args (tail args)) $ \(src, snk) ->
      case gGrow f False (graph dict src) (graph dict snk) of
        Nothing -> T.putStrLn $ T.pack ("  " <> show src <> "; " <> show snk <> ";")
        Just es -> forM_ (S.toList es) $ \(a, b) ->
          T.putStrLn $ T.pack ("  " <> show a <> " -> " <> show b <> ";")
  putStrLn "}"

readDict :: IO (Set Word)
readDict = do
  d <- T.readFile dictFile
  return . S.fromList . map T.toUpper . filter (\w -> T.all isLower w && 1<T.length w) . T.lines $ d
  where
    dictFile = "/usr/share/dict/words"

vowels, consonants, phonemes :: [T.Text]
vowels = T.words "AA AE AH AO AW AY EH ER EY IH IY OW OY UH UW"
consonants = T.words "B CH D DH F G HH JH K L M N NG P R S SH T TH V W Y Z ZH"
phonemes = vowels ++ consonants

I also implemented the O(V³) Floyd-Warshall algorithm for finding the longest shortest paths in the entire pronunciation adjacency graph of the intersection between the CMUDict and the all-lower-case words in /usr/share/dict/words, in C running on 16 cores it still took over 4 hours to run. I should have spent the 8 hours (because I ran it twice, with slightly different adjacency classes) finding and implementing a faster algorithm, apparently it can be done in O(E V α(E, V)) which is much much better:

Computing shortest paths with comparisons and additions.

Pettie, Seth; Ramachandran, Vijaya (2002).

Proceedings of the thirteenth annual ACM-SIAM symposium on Discrete algorithms. pp. 267–276. ISBN 0-89871-513-X.

Abstract We present an undirected all-pairs shortest paths (APSP) algorithm which runs on a pointer machine in time O(mnα(m,n)) while making O(mnlog α(m, n)) comparisons and additions, where m and n are the number of edges and vertices, respectively, and α(m, n) is Tarjan's inverse-Ackermann function. This improves upon all previous comparison & addition-based APSP algorithms when the graph is sparse, i.e., when m = o(n log n).At the heart of our APSP algorithm is a new single-source shortest paths algorithm which runs in time O(mα(m, n) + n log log r) on a pointer machine, where r is the ratio of the maximum-to-minimum edge length. So long as r < 2no(1) this algorithm is faster than any implementation of Dijkstra's classical algorithm in the comparison-addition model.For directed graphs we give an O(m + n log r)-time comparison & addition-based SSSP algorithm on a pointer machine. Similar algorithms assuming integer weights or the RAM model were given earlier.

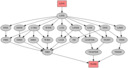
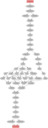
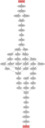
The longest shortest paths are of length 26, here's the output images:

Here's the C code (note: needs 7GB RAM for this (hardcoded) size graph):

#include <stdint.h>
#include <stdio.h>

#define INFINITY 65535

#define V 42447

uint16_t a[2][V][V];

int diameter(void)
{
  for (int k = 0; k < V; ++k)
  {
    fprintf(stderr, "\r%d", k);
    int src = k & 1;
    int dst = 1 - src;
    #pragma omp parallel for
    for (int i = 0; i < V; ++i)
      for (int j = 0; j < V; ++j)
        a[dst][i][j] = a[src][i][j];
    #pragma omp parallel for
    for (int i = 0; i < V; ++i)
    {
      uint32_t ik = a[src][i][k];
      if (ik < INFINITY)
      {
        for (int j = 0; j < V; ++j)
        {
          uint32_t kj = a[src][k][j];
          if (kj < INFINITY)
          {
            uint32_t ij = a[src][i][j];
            uint32_t d = ik + kj;
            if (ij > d)
            {
              a[dst][i][j] = d;
            }
          }
        }
      }
    }
  }
  int src = V & 1;
  int m = 0;
  #pragma omp parallel for reduction(max:m)
  for (int i = 0; i < V; ++i)
  {
    int mi = 0;
    for (int j = 0; j < V; ++j)
    {
      int x = a[src][i][j];
      if (x < INFINITY)
        mi = x > mi ? x : mi;
    }
    m = mi > m ? mi : m;
  }
  return m;
}

int main()
{
  fread(&a[0][0][0], sizeof(a[0][0][0]) * V * V, 1, stdin);
  int m = diameter();
  printf("%d\n", m);
  int src = V & 1;
  for (int i = 0; i < V; ++i)
    for (int j = i; j < V; ++j)
      if (a[src][i][j] == m)
        printf("%d %d\n", i, j);
  return 0;
}

And supporting Haskell code:

adjMatrix :: Set Text -> (Text -> [Text]) -> ST s (STUArray s (Int, Int) Word16)
adjMatrix dict f = do
  v <- pure $ S.size dict - 1
  a <- newArray ((0,0),(v,v)) maxBound
  forM_ ([0 .. v] `zip` S.toList dict) $ \(i, p) -> do
    writeArray a (i, i) 0
    forM_ (f (S.elemAt i dict)) $ \w -> do
      let j = S.findIndex w dict
      when (i /= j) $ do
        writeArray a (i, j) 1
        writeArray a (j, i) 1
  return a

floydWarshall :: Set Text -> (Text -> [Text]) -> IO (Int, [(Text, Text)])
floydWarshall dict f = do
  let a :: UArray (Int, Int) Word16
      a = runSTUArray (adjMAtrix dict f)
      v = Data.Vector.Storable.fromListN (S.size dict^2) (A.elems a)
  withCreateProcess ((proc "./a.out" [])
      { std_in = CreatePipe, std_out = Inherit, std_err = Inherit }
    ) $ \(Just hin) _ _ ph -> do
    forkIO $ V.unsafeWith v (\p ->
      hPutBuf hin p (sizeOf (0 :: Word16) * S.size dict ^ 2))
    waitForProcess ph
  return (maxBound, [])
-- get stdout and paste (modified) into code like this
-- didn't manage to get parsing working properly
{-
  let e x = S.elemAt x dict
      f x y = (e x, e y)
  return (26,
    [f 15021 30928
    ,f 15021 33278
    ,f 15021 33279
    ,f 15021 35870
    ,f 15021 37719
    ,f 28802 30928
    ,f 28802 33278
    ,f 28802 33279
    ,f 30667 30928
    ,f 30667 33278
    ,f 30667 33279
    ])
-}

If there are any other (better) pronouncing dictionaries out there, let me know - especially if they have nice free/open licenses - as the CMUDict has some idiosyncracies.