Parallel transport in hyperbolic tilings

Hyperbolic Geometry is "the other kind of hyperspace" - instead of higher-dimensional but still flat Euclidean space - that I've been playing around a bit with this year. Negatively curved space is weird, there is "much more" space the further you go from your starting point. Hard to explain without lots of diagrams and physical models that come to pieces and bearded sandle-wearing lecturers all in tasteful shades of orange and brown. Not much of this work/play has born productive fruit, mostly because I don't think I understand it much at all yet.

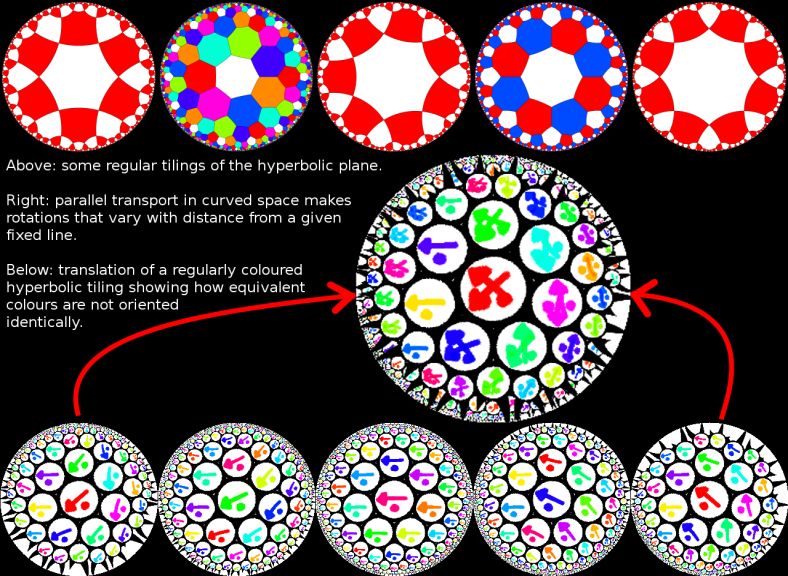
Hyperbolic Plane Tilings (covering the hyperbolic plane with identical regular polygons) turn out to be interesting (for some values of interesting). Triangles in hyperbolic space have angle sum less than 180 degrees (or pi radians). The angle defect (how much less the sum is) depends on the area of the triangle - the longer a triangle's sides the smaller its angles are. I'll spare the equations... Regular polygons can be made up of lots of congruent right-angled triangles (you split a p-gon into 2p triangles with the right-angles at the midpoints of the p-gon's edges) even in hyperbolic space. Combining the ability to pick the angle sum (and thus the two other angles) of a right-angled triangle by varying its size with polygon triangulation, it's possible to tile the hyperbolic plane with regular polygons in many more ways than than is possible in flat space or on a sphere.

Colouring Hyperbolic Tilings turns out to be quite a challenge. I'll go into more detail in a later post, but for example when you colour the {7,3} tiling with 8 colours each spread regularly across the whole plane, you find that some of the 7-gons that are coloured the same have their neighbouring colours in a different order around them. If you take this into account you can colour {7,3} with 24 colours and be satisfied that it's a perfect colouring, but similarly simple tilings require a mindnumbingly huge number of colours to achieve the same goal.

Animating Coloured Hyperbolic Tilings is the eventual goal of all of this, and while I have some preliminary results there's an annoying glitch where the rotations don't line up at the animation loop point. This is caused by parallel transport. I think. At least I don't have any other explanation at this stage! EDIT (2008-12-27) I discovered the real cause: the "initial conditions" where all arrows were aligned in Euclidean space. Having switched the code to align each tile relative to its neighbouring tiles I have smooth looping!

Parallel Transport is a concept that arises when you think of the effect moving around inside a space has on your internal notion of direction. In flat space, no matter which route you take they all match up. In fact a definition of curved space is that your internal notion of direction when you move through it depends on which route you took. In the hyperbolic plane you get a rotation proportional to the area of the loop you travel in.

Source code (currently a bit of a mess, probably missing stuff too) implemented in Haskell and mostly undocumented and horribly flawed is here:

svn co https://code.goto10.org/svn/maximus/2008/bolix bolix