mathr / blog / #

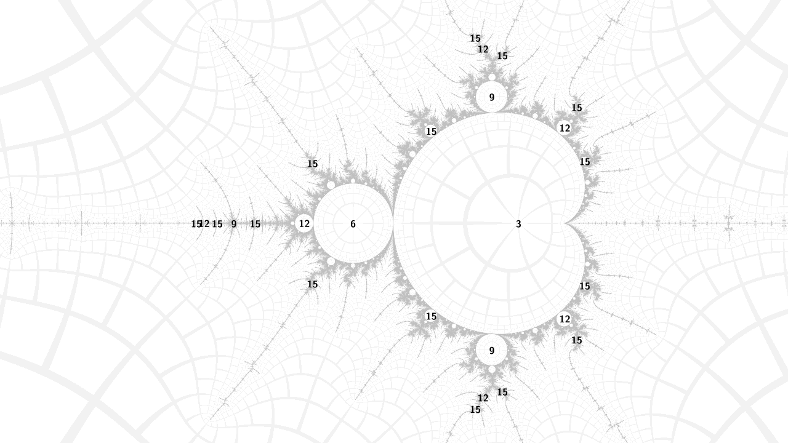
The Mandelbrot set contains hyperbolic components (cardioid-like and circle-like regions), each with a super-attracting periodic nucleus at its center. The image above labels some with their periods (click for bigger).

The Mandelbrot set contains smaller copies of itself, with the periods all multiplied by a factor. The image above is the period 3 island in the antenna of the main set. The multiplication is called tuning or renormalization, and occurs because \(P\) iterations of \(z^2 + c\) are locally equivalent to \(1\) iteration of \(Z^2 + C\) where \(Z, C\) are a linear change of variable from \(z, c\).

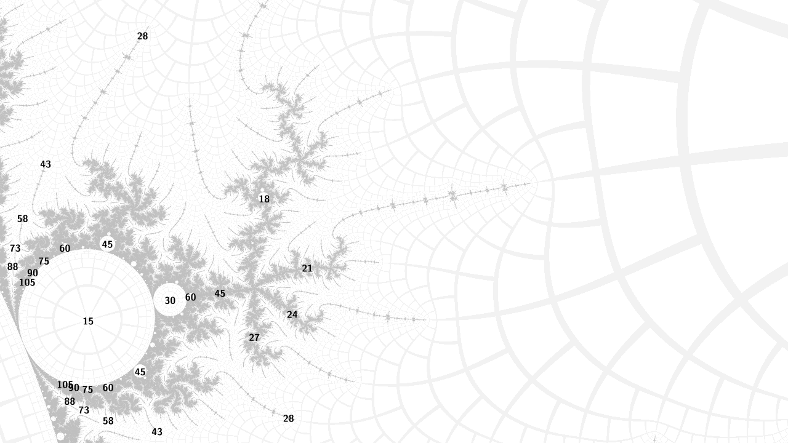
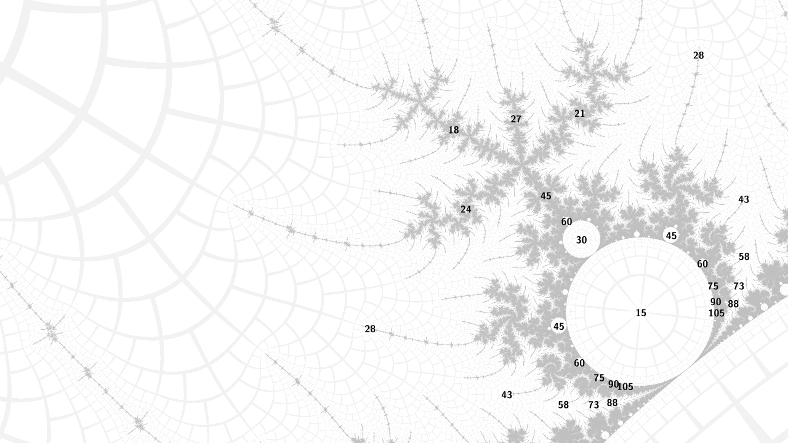
Above are the two upper period 15 child bulbs at internal angles 1/5 and 2/5, with parent the period 3 cardioid. You can see that the islands in the primary antennae (of which there are 5) attached to the 1/5 bulb go up by 3 in period when you go 1 step around, but the corresponding ones of the 2/5 bulb go up by 3 in period when you go 2 steps around. This is described in the paper:

Geometry of the Antennas in the Mandelbrot Set

R.L. Devaney and M. Moreno-Rocha

April 11, 2000

In the Mandelbrot set, the bulbs attached directly to the main cardioid are called the p/q -bulbs. The reason for this is that the largest component of the interior of these bulbs consists of c-values for which the quadratic function \(Q_c (z) = z^2 + c\) admits an attracting cycle with rotation number p/q. In this paper we give a geometric method to read off p/q from the geometry of the antenna attached to the bulb.

The island copies are decorated with hairy filaments, and around islands in the hairs are embedded Julia sets, structures of filaments that look similar to Julia sets at the corresponding location to the influencing island. Hairs in the "seahorse valley" of an island will have embedded Julia sets that look like those for parameters in the "seahorse valley" of the main part of the Mandelbrot set (near \(-0.75 + 0.00 i\)).

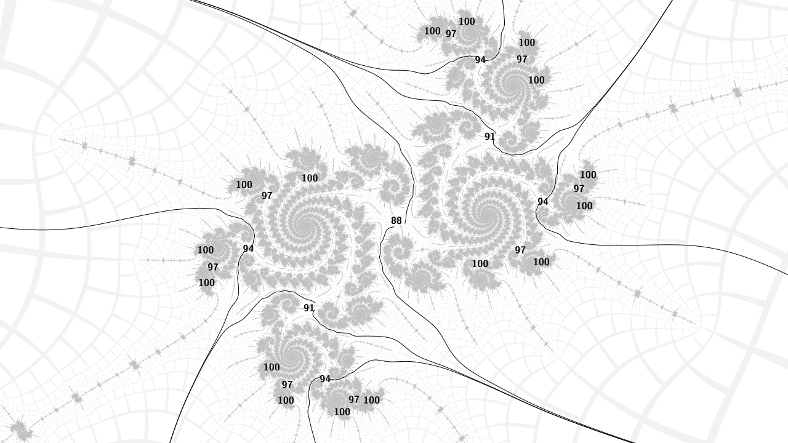
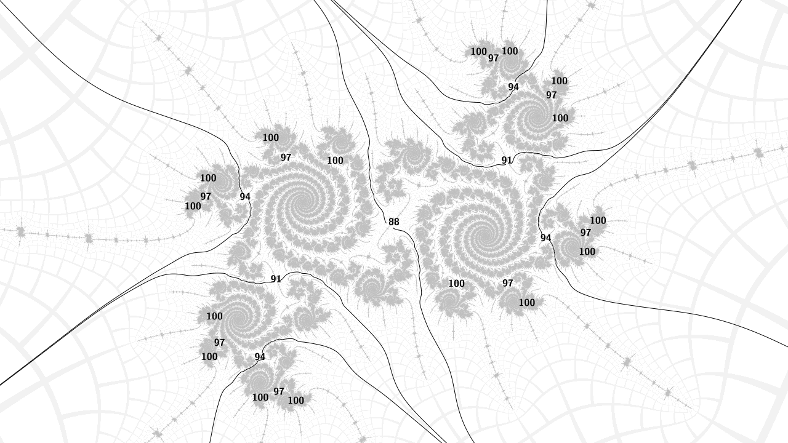
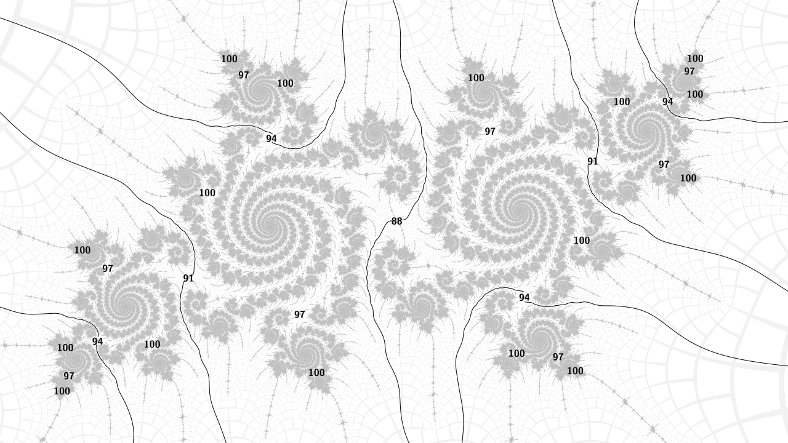
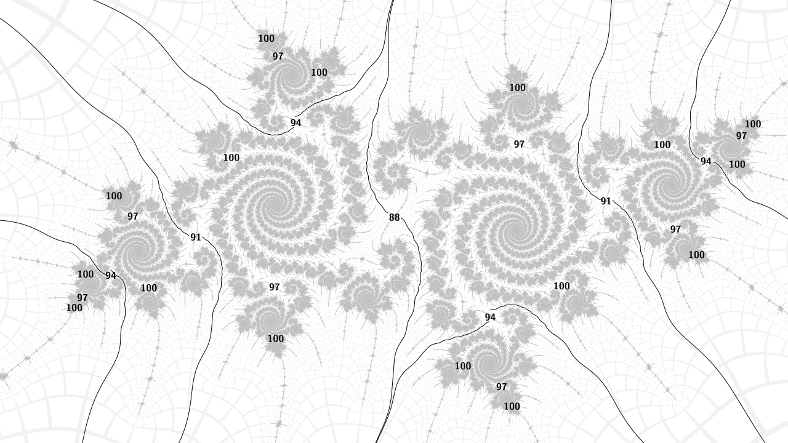
This pattern carries over to the embedded Julia sets surrounding the period 88 islands in the hairs either side of the period 15 bulbs. Above are the 1/5, the periods go up by 3 going 1 step around the spirals with 5 arms. Below are the 2/5, the periods go up by 3 going 2 steps around the spirals. Note also that the spirals turn in opposite ways according to which side of the bulb the embedded Julia set is, but the direction of increase of the periods is the same in both cases.

Finally, note that the rays at each increasing period divide the embedded Julia set in half, and there is one island of period 3 higher in each part. So there is 1 island of period 88, 2 of 91, 4 of 94, 8 of 97, and so on. This binary subdivision property is not unique to these specific Julia sets. I conjecture that it holds for all of them, apart from possibly those in the filaments heading to the cardioid cusp or from the antenna tip of an island.

Future work includes investigating more embedded Julia sets to check that the conjecture holds, possibly proving it via combinatorial arguments to do with external angles and rays, and extending the investigation to doubly embedded Julia sets which appear when passing close to two islands in a deeper zoom.

PS: the diagrams were made with the new GTK GUI for mandelbrot-perturbator, which I ported from my old book project code. I added "plain" rendering to the library too, it's much faster at low zoom levels, especially because of the interior checking (I still need to add interior checking to the perturbation codepath...). You can download the parameters used for the images in this post: patterns-in-embedded-julia-sets.tbz.