mathr / blog / #

Previously I wrote about an automated Julia morphing method extrapolating patterns in the binary representation of external angles, and then tracing external rays. However this was impractical as it was \(O(p^2)\) for final period \(p\) and the period typically more than doubles at each next level of morphing. This week I devised an \(O(p)\) algorithm, which requires a little bit of setting up and doesn't always work but when it works it works very well.

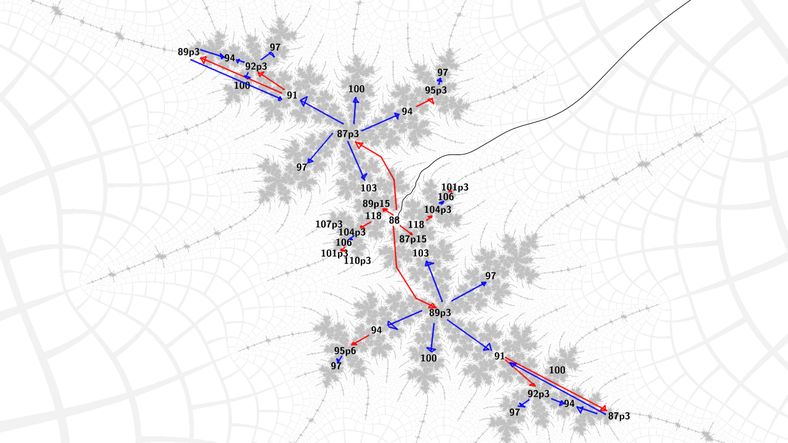
The first key insight was that in embedded Julia sets, the primary spirals and tips are distinguishable by the preperiods of the Misiurewicz points at their centers. Moreover when using the "full" Newton's method algorithm for Misiurewicz points that rejects lower preperiods by division, the basins of attraction comfortably enclose the center of the embedded Julia set itself.

So, we can choose the appropriate (pre)period to get to the center of the spiral either inwards towards the main body of the Mandelbrot set or outwards towards its tips. Now, from a Misiurewicz center of a spiral, Newton's method for periodic nucleus finding will work for any of the periods that form the structural spine of the spiral - these go up by a multiple of the period of the influencing island. From these nuclei we can jump to the Misiurewicz spiral on the other side, using Newton's method again. In this way we can algorithmically find any nucleus or Misiurewicz point in the structure of the embedded Julia set.

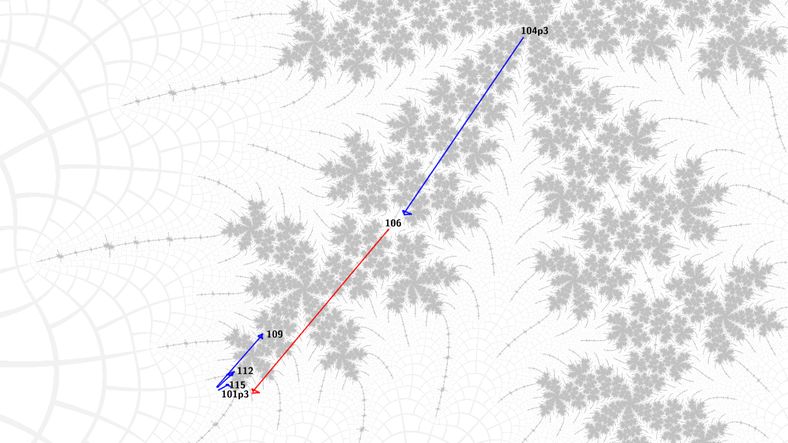
Some images should make this clearer at this point: blue means Newton's method for nucleus, red means Newton's method for Misiurewicz point, nuclei are labeled with their period, Misiurewicz points with preperiod and period in that order, separated by 'p'.

The second key insight was that the atom domain coordinate of the tip of the treeward branch at each successive level was scaled by a power of 1.5 from the one at the previous level. Because atom domain coordinates correspond to the unit disc, this means they are closer to the nucleus. This allowed an initial guess for finding the Misiurewicz point at the tip more precisely (the first insight does only apply to "top-level" embedded Julia sets, not their morphings - there is a "symmetry trap" that breaks Newton's method because the boundary of the basins of attraction passes through the point we want to start from). I implemented a Newton's method iteration to find a point with a given atom domain coordinate. This relationship is only true in the limit, so the input to the automatic morphing algorithm starts at the first morphing, rather than the top level embedded Julia set.

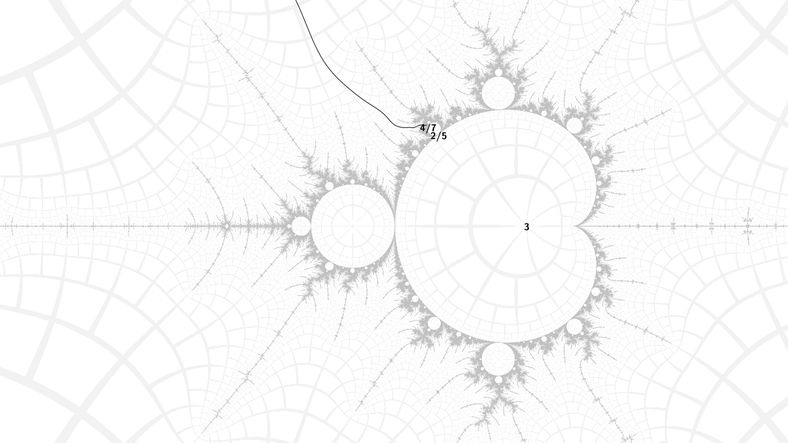
My first test was quite challenging: to morph a tree with length 7 arms, from an embeddded Julia set at angled internal address:

1_1/2→2_1/2→3_2/5→15_4/7→88

The C code (full link at the bottom) that sets up the parameters for this morphing looks like this:

#ifdef EXAMPLE_1
  const char *embedded_julia_ray = ".011100011100011011100011011100011100011100011011100011011100011100011100011011100011100001110001101110010010010010010010010001110001110001101110001101110001110001110001101110001101110001110001110001101110001110000111000110111(001)";
  int ray_preperiod = 225;
  int ray_period = 3;
  double _Complex ray_endpoint
    = -1.76525599938987623396492597243303e+00
    +  1.04485517375987067290733632798876e-02 * I;
  int influencing_island_period = 3;
  int embedded_julia_set_period = 88;
  int denominator_of_rotation = 5;
  int arm_length = 7;
  double view_size_multiplier = 3600;
#endif

The ray lands on the treeward-tip Misiurewicz point of the first morphed Julia set, this end point is cached to avoid long ray tracing computations. The next 4 numbers are involved in the iterative morphing calculations of the relevant periods and preperiods, with the arm length being the primary variable to adjust once the Julia set is found. The view size multiplier sets how to zoom out from the central morphed figure to frame the result nicely, maybe I can find a good heuristic to determine this based on arm length.

The morphing looks like this:

The second example is similar, starting with the island with this angled internal address, with tree morphing arm length 9.

1_1/2→2_1/2→3_1/2→4_1/2→8_1/15→116_1/2→119

The third and final example (for now) is simpler still, starting at the island with this internal address, with tree morphing arm length 1.

1_1/3→3_1/2→4_11/23→89

The code for example 3 contains an ugly hack, because the method for guessing the location of the next Misiurewicz point (for starting Newton's method iterations) isn't good enough - the radius is accurate, but the angle is not - my atom domain coordinate method is clearly not the correct one in general...

Here are the timings in seconds for calculating the coordinates (not parallelized) and rendering the images (I used m-perturbator-offline at 1280x720, the parallel efficiency is somewhat low because it doesn't know the center point is already a good reference and it tries to find one in the view - it would be much faster if I let it take the primary reference as external input - more things TODO):

morph	coordinates			image rendering
	eg1	eg2	eg3	eg1		eg2		eg3
				real	user	real	user	real	user
1	0	0	0	0.633	2.04	0.625	2.00	0.551	1.74
2	0	0	0	0.817	2.41	0.943	2.31	0.932	3.19
3	0	0	0	1.16	3.56	1.43	4.53	1.26	4.19
4	1	0	0	1.37	4.38	1.86	6.06	1.73	5.86
5	1	2	1	2.29	7.45	3.43	11.4	2.67	8.78
6	2	4	2	3.95	12.3	5.73	18.4	4.26	14.9
7	10	14	2	7.42	23.6	8.66	26.7	6.90	21.1
8	24	37	7	28.2	95.1	42.4	142	12.6	36.4
9	92	155	27	63.7	257	92.6	292	21.5	63.5
10	288	442	51	141	419	207	609	77.5	263
total	418	654	90	259	774	372	1120	137	430

The code is part of my mandelbrot-numerics project. You also need my mandelbrot-symbolics project to compile the example program, and you may also want mandelbrot-perturbator to render the output (note: the GTK version is currently hardcoded to 65536 maximum iteration count, which isn't enough for deeper morphed Julia sets - adding runtime configuration for this is my next priority). Other deep zoomers are available, for example my Kalles Fraktaler 2 + GMP fork with Windows binaries available (that also work in WINE on Linux).